题目内容
某工艺厂开发一种新工艺品,头两天试制中,该厂要求每位师傅每天制作10件,该厂质检部每天从每位师傅制作的10件产品中随机抽取4件进行检查,若发现有次品,则当天该师傅的产品不能通过.已知李师傅第一天、第二天制作的工艺品中分别有2件、1件次品.
(1)求两天中李师傅的产品全部通过检查的概率;
(2)若厂内对师傅们制作的工艺品采用记分制,两天都不通过检查的得0分,两天中只通过一天检查的得1分,两天都通过检查的得2分,求李师傅在这两天内得分的数学期望.
(1)  ;(2)
;(2) 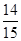 .
.
解析试题分析:(1)根据独立事件的交事件概率为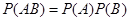 进行计算即可.设李师傅产品第一天通过检查为事件A;第二天产品通过检查为事件B.
进行计算即可.设李师傅产品第一天通过检查为事件A;第二天产品通过检查为事件B.
则有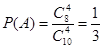 ,
,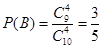 ,故
,故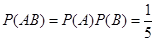 .
.
(2)根据离散型随机变量的期望公式计算.记得分为ξ,则ξ的可能值为0,1,2.
P(ξ=0)=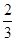 ×
×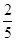 =
=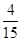 ; P(ξ=1)=
; P(ξ=1)=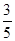 ×
×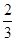 +
+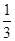 ×
×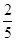 =
=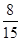 ; P(ξ=2)=
; P(ξ=2)=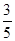 ×
×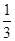 =
=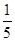 .
.
E(ξ)=0×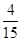 +1×
+1×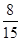 +2×
+2×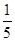 =
=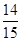 .
.
(1)设李师傅产品第一天通过检查为事件A;第二天产品通过检查为事件B.
则有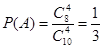 ,P(B)=
,P(B)=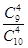 =
=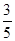 , (4分)
, (4分)
由事件A、B独立,∴P(AB)=P(A)P(B)= . (6分)
. (6分)
答:李师傅这两天产品全部通过检查的概率为 .
.
(2)记得分为ξ,则ξ的可能值为0,1,2. (7分)
∵P(ξ=0)=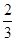 ×
×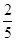 =
=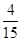 ; (8分 P(ξ=1)=
; (8分 P(ξ=1)=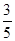 ×
×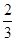 +
+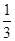 ×
×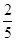 =
=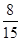 ; (9分)
; (9分)
P(ξ=2)=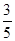 ×
×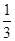 =
=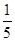 . ( 10分)
. ( 10分)
∴E(ξ)=0×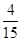 +1×
+1×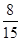 +2×
+2×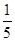 =
=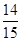 . (12分)
. (12分)
考点:随机事件及其概率、概率的基本事件(互斥事件、对立事件)、离散型随机变量的期望.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 ,
, ,
,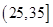 ,
,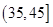 ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图. 的值;
的值; 组的频率为
组的频率为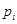 ,第
,第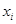
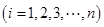 ,则样本数据的平均值为
,则样本数据的平均值为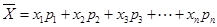 .)
.) ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取
,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取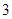 天的数值,其中达到“特优等级”的天数为
天的数值,其中达到“特优等级”的天数为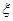 ,求
,求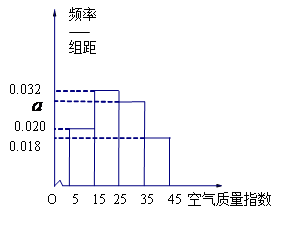
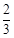 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.(12分)
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.(12分)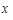 的分布列和数学期望.
的分布列和数学期望.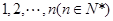 从小到大排列构成一个数
从小到大排列构成一个数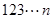 ,
,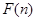 为这个数的位数(如
为这个数的位数(如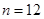 时,此数为
时,此数为 ,共有15个数字,
,共有15个数字, ),现从这个数中随机取一个数字,
),现从这个数中随机取一个数字,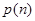 为恰好取到0的概率.
为恰好取到0的概率.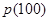 ;
;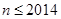 时,求
时,求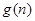 为这个数中数字0的个数,
为这个数中数字0的个数,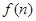 为这个数中数字9的个数,
为这个数中数字9的个数,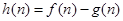 ,
, ,求当
,求当 时
时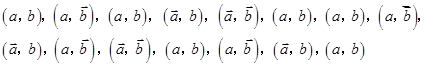
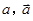 分别表示甲组研发成功和失败;
分别表示甲组研发成功和失败;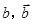 分别表示乙组研发成功和失败.
分别表示乙组研发成功和失败.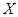 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 棵,梧桐树
棵,梧桐树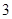 棵.它们移栽后的成活率分别
棵.它们移栽后的成活率分别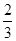 、
、 ,每棵树是否存活互不影响,在移栽的
,每棵树是否存活互不影响,在移栽的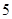 棵树中:
棵树中: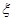 的分布列与期望.
的分布列与期望.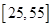 岁的人群中随机抽取n人进行了一次调查,得到如下统计表:
岁的人群中随机抽取n人进行了一次调查,得到如下统计表: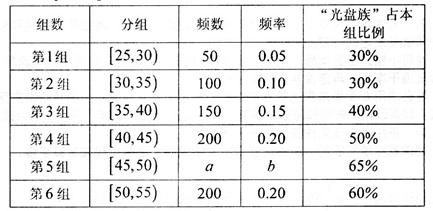
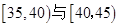 的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.
的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.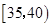 中的前提下,求另一人来自年龄段
中的前提下,求另一人来自年龄段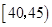 中的概率;
中的概率;