题目内容
7.已知f(x)=$\frac{m}{x+1}$+nlnx(m,n为常数),在x=1处的切线方程为x+y-2=0.(Ⅰ)求f(x)的解析式并写出定义域;
(Ⅱ)若?x∈[$\frac{1}{e}$,1],使得对?t∈[$\frac{1}{2}$,2]上恒有f(x)≥t3-t2-2at+2成立,求实数a的取值范围.
分析 (Ⅰ)利用导数的几何意义求得m,n的值,根据对数函数的定义得到函数定义域;
(Ⅱ)f(x)在[$\frac{1}{e}$,1]上的最小值为f(1)=1,只需t3-t2-2at+2≤1,即$2a≥{t^2}-t+\frac{1}{t}$对任意的$t∈[\frac{1}{2},2]$上恒成立,构造函数m(t),利用导数求出m(t)的最大值,即可求得结论.
解答 解:(Ⅰ)由$f(x)=\frac{m}{x+1}+nlnx$可得$f'(x)=-\frac{m}{{{{(x+1)}^2}}}+\frac{n}{x}$,
由条件可得$f'(1)=-\frac{m}{4}+n=-1$,
把x=-1代入x+y=2可得,y=1,
∴$f(1)=\frac{m}{2}=1$,∴m=2,$n=-\frac{1}{2}$,
∴$f(x)=\frac{2}{x+1}-\frac{1}{2}lnx$,(0,+∞);
(Ⅱ)由(Ⅰ)知f(x)在$[\frac{1}{e},1]$上单调递减,
∴f(x)在$[\frac{1}{e},1]$上的最小值为f(1)=1,
故只需t3-t2-2at+2≤1,即$2a≥{t^2}-t+\frac{1}{t}$对任意的$t∈[\frac{1}{2},2]$上恒成立,
令m(t)=${t^2}-t+\frac{1}{t}$,
易求得m(t)在$[\frac{1}{2},1]$单调递减,[1,2]上单调递增,
而$m(\frac{1}{2})=\frac{7}{4}$,$m(2)=\frac{5}{2}$,
∴2a≥m(t)max=g(2)
∴$a≥\frac{5}{4}$,即a的取值范围为$[\frac{5}{4},+∞)$.
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了恒成立问题的等价转化方法,属于中档题.

| A. | 若m、n都平行于平面α,则m、n一定不是相交直线. | |
| B. | m、n在平面α内的射影互相垂直,则m、n互相垂直 | |
| C. | 若m、n都垂直于平面α,则m、n一定是平行直线. | |
| D. | 已知α、β互相垂直,m、n互相垂直,若m⊥α,则n⊥β |
| A. | 35 | B. | 32 | C. | 30 | D. | 27 |
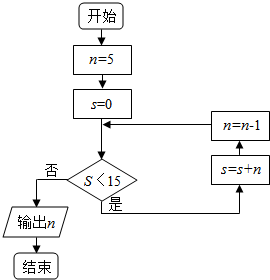
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | $?x∈[{\frac{π}{2},π}],sinx-cosx<2$ | B. | $?x∈[{\frac{π}{2},π}],sinx-cosx≤2$ | ||
| C. | $?x∈[{\frac{π}{2},π}],sinx-cosx≤2$. | D. | $?x∈[{\frac{π}{2},π}],sinx-cosx<2$ |
| A. | $\frac{1}{2k+2}$ | B. | $\frac{1}{2k+1}$+$\frac{1}{2k+2}$ | C. | $\frac{1}{2k+1}$-$\frac{1}{2k+2}$ | D. | $\frac{1}{2k+1}$-$\frac{3}{2k+2}$ |