题目内容
已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N,都能使m整除f(n),求m的最大值。
m值等于36
∵f(1)=36,f(2)=108=3×36,f(3)=360=10×36
∴f(1),f(2),f(3)能被36整除,猜想f(n)能被36整除.
证明:n=1,2时,由上得证,设n=k(k≥2)时,
f(k)=(2k+7)·3k+9能被36整除,则n=k+1时,
f(k+1)-f(k)=(2k+9)·3k+1?-(2k+7)·3k
=(6k+27)·3k-(2k+7)·3k
=(4k+20)·3k=36(k+5)·3k-2?(k≥2)
 f(k+1)能被36整除
f(k+1)能被36整除
∵f(1)不能被大于36的数整除,∴所求最大的m值等于36
∴f(1),f(2),f(3)能被36整除,猜想f(n)能被36整除.
证明:n=1,2时,由上得证,设n=k(k≥2)时,
f(k)=(2k+7)·3k+9能被36整除,则n=k+1时,
f(k+1)-f(k)=(2k+9)·3k+1?-(2k+7)·3k
=(6k+27)·3k-(2k+7)·3k
=(4k+20)·3k=36(k+5)·3k-2?(k≥2)
 f(k+1)能被36整除
f(k+1)能被36整除∵f(1)不能被大于36的数整除,∴所求最大的m值等于36

练习册系列答案
相关题目
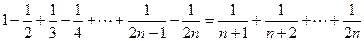
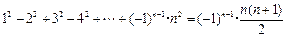 .
.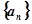 的前
的前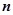 项和为
项和为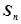 ,满足
,满足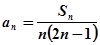 ,且
,且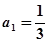 .
.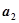 ,
,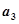 ,
,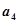 ;
; 为常数,且
为常数,且

 有
有 ,求
,求 ,则函数
,则函数 的最大值为( )
的最大值为( )



 成立,起始值至少应取为( )
成立,起始值至少应取为( )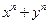 能被
能被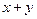 整除”,在第二步时,正确的证法是( )
整除”,在第二步时,正确的证法是( )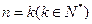 ,证明
,证明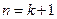 命题成立
命题成立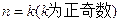 ,证明
,证明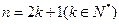 ,证明
,证明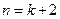 命题成立
命题成立