题目内容
已知数列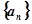 的前
的前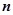 项和为
项和为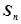 ,满足
,满足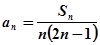 ,且
,且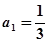 .
.
(Ⅰ)求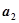 ,
,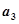 ,
,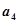 ;
;
(Ⅱ)猜想数列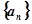 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.
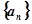 的前
的前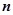 项和为
项和为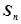 ,满足
,满足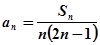 ,且
,且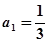 .
.(Ⅰ)求
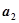 ,
,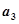 ,
,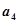 ;
;(Ⅱ)猜想数列
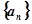 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.(Ⅰ) ;
; ;
; .
.
(Ⅱ)猜想数列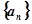 的通项公式为
的通项公式为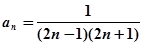 .
.
下面用数学归纳法进行证明:
(1) 当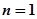 时,
时, ,猜想成立.
,猜想成立.
(2) 假设当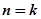 时,
时,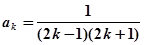 成立,
成立,
则当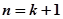 时,由
时,由 ,得
,得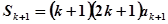
由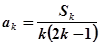 ,得
,得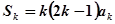
两式作差得:
即
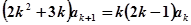
 ,所以猜想成立.
,所以猜想成立.
综上所述,对一切正的自然数都有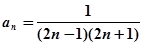
 ;
; ;
; .
.(Ⅱ)猜想数列
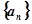 的通项公式为
的通项公式为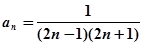 .
.下面用数学归纳法进行证明:
(1) 当
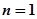 时,
时, ,猜想成立.
,猜想成立.(2) 假设当
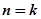 时,
时,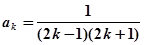 成立,
成立,则当
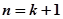 时,由
时,由 ,得
,得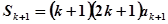
由
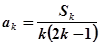 ,得
,得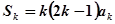
两式作差得:

即

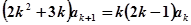
 ,所以猜想成立.
,所以猜想成立.综上所述,对一切正的自然数都有
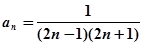
略

练习册系列答案
相关题目
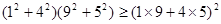 ;
;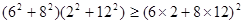 ;
;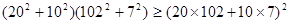 .
.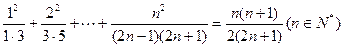 。
。 的表达式表示
的表达式表示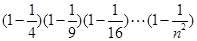 的值,并用数学归纳法证明你的结论.
的值,并用数学归纳法证明你的结论.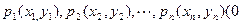 <
<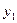 <
<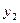 <…<
<…<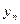 )是曲线C
)是曲线C
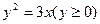 上的n个点,点
上的n个点,点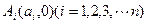 在x轴的正半轴上,且⊿
在x轴的正半轴上,且⊿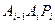 是正三角形(
是正三角形(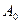 是坐标原点)。
是坐标原点)。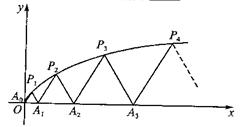
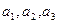
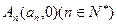 的横坐标
的横坐标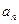 关于n的表达式并用数学归纳法证明
关于n的表达式并用数学归纳法证明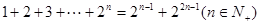 时,假设n=k时命题成立,则当n=k+1时,左端增加的项数是 ( )
时,假设n=k时命题成立,则当n=k+1时,左端增加的项数是 ( )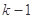 项
项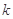 项
项 项
项