题目内容
8.已知椭圆E的两焦点分别为(-1,0)(1,0),且经过点(1,$\frac{\sqrt{2}}{2}$)(Ⅰ)求椭圆E的方程;
(Ⅱ)过P(-2,0)的直线l交E于A、B两点,且$\overrightarrow{PB}$=3$\overrightarrow{PA}$,设A、B两点关于x轴的对称点分别是C、D,求四边形ACDB的外接圆的方程.
分析 (Ⅰ)由题意可得c=1,进而可得a2=b2+1,把点(1,$\frac{\sqrt{2}}{2}$)代入$\frac{{x}^{2}}{{b}^{2}+1}$+$\frac{{y}^{2}}{{b}^{2}}$=1可得系数,可得方程;
(Ⅱ)设l:x=my-2,代入椭圆E$\frac{{x}^{2}}{2}$+y2=1并整理可得(m2+2)y2-4my+2=0,由韦达定理可得m2=4不妨取m=2可得圆心和半径,可得方程.
解答 解:(Ⅰ)由题意可得c=1,∴a2=b2+1,
把点(1,$\frac{\sqrt{2}}{2}$)代入$\frac{{x}^{2}}{{b}^{2}+1}$+$\frac{{y}^{2}}{{b}^{2}}$=1可得$\frac{1}{{b}^{2}+1}$+$\frac{1}{2{b}^{2}}$=1,
解得b2=1,∴a2=b2+1=2,
∴椭圆E的方程为$\frac{{x}^{2}}{2}$+y2=1;
(Ⅱ)由题意设l:x=my-2,代入椭圆E$\frac{{x}^{2}}{2}$+y2=1并整理可得(m2+2)y2-4my+2=0,
由△=16m2-8(m2+2)>0可解得m2>2,
设A(x1,y1),B(x2,y2),则y1+y2=$\frac{4m}{{m}^{2}+2}$,①y1y2=$\frac{2}{{m}^{2}+2}$,②,
由$\overrightarrow{PB}$=3$\overrightarrow{PA}$可得y2=3y1,③,由①②③解得m2=4符合m2>2
不妨取m=2,则线段AB的垂直平分线方程为y=-2x-$\frac{2}{3}$,
则所求圆的圆心为(-$\frac{1}{3}$,0),又可得B(0,1),
∴圆的半径r=$\frac{\sqrt{10}}{3}$
∴所求圆的方程为(x+$\frac{1}{3}$)2+y2=$\frac{10}{9}$
点评 本题考查直线与圆锥曲线的位置关系,设计椭圆的标准方程和圆的知识,属中档题.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案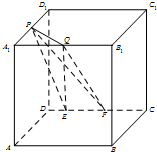 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )| A. | 点P到平面QEF的距离 | B. | 三棱锥P-QEF的体积 | ||
| C. | 直线PQ与平面PEF所成的角 | D. | 二面角P-EF-Q的大小 |
 满足
满足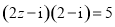 ,则
,则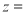 ( )
( )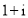 B.
B.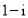
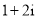 D.
D.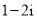
 的公差为
的公差为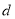 ,前
,前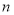 项和为
项和为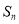 ,若
,若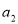 ,
,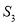 ,
,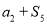 成等比数列,则
成等比数列,则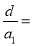 ( )
( )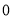 B.
B.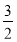
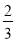 D.
D.