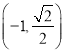题目内容
【题目】已知斜率存在且不为0的直线![]() 过点
过点![]() ,设直线
,设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,椭圆
两点,椭圆![]() 的左顶点为
的左顶点为![]() .
.
(1)若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若直线![]() 分别交直线
分别交直线![]() 于点
于点![]() ,且
,且![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .探究:
.探究:![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
【答案】(1)![]() 或
或![]() . (2)是,定值为
. (2)是,定值为![]()
【解析】
(1)设![]() ,
,![]() ,设直线
,设直线![]() ,根据题意求出
,根据题意求出![]() ,由
,由![]() 求出
求出![]() , 联立直线方程与椭圆方程,利用韦达定理求出
, 联立直线方程与椭圆方程,利用韦达定理求出![]() 即可;
即可;
(2)设直线![]() 的方程为:
的方程为:![]() 与椭圆方程联立得到关于
与椭圆方程联立得到关于![]() 的一元二次方程,设
的一元二次方程,设![]() ,
,![]() ,利用韦达定理求出
,利用韦达定理求出![]() ,利用点斜式求出直线
,利用点斜式求出直线![]() 的方程,进而求出点
的方程,进而求出点![]() 坐标,利用平面向量坐标表示求出
坐标,利用平面向量坐标表示求出![]() 的表达式,代入斜率公式求出直线
的表达式,代入斜率公式求出直线![]() 的斜率即可求解.
的斜率即可求解.
(1)设![]() ,
,![]() ,
,
因为![]() ,椭圆
,椭圆![]() 的左顶点为
的左顶点为![]() ,所以
,所以![]() ,
,
故![]() ,
,
故![]() ,
,
设直线![]() ,代入椭圆
,代入椭圆![]() 的方程中,整理得
的方程中,整理得![]() ,
,
所以![]() ,
,![]() ,
,
故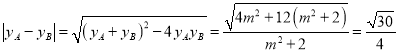 ,
,
解得![]() ,
,![]() ,
,
故直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(2)由题意得,设直线![]() 的方程为:
的方程为:![]() ,
,
与椭圆方程联立可得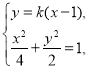 ,
,
整理得![]() ,
,
设![]() ,
,![]() ,
,
则![]() ①,
①,![]() ②,
②,
又![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
令![]() ,解得
,解得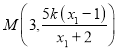 ,
,
同理可得,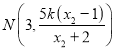 ,设
,设![]() ,
,
所以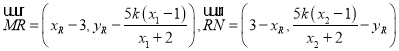 ,
,
因为![]() ,所以
,所以![]() ,
,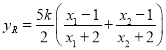 ,
,
将①②代入上式并化简可得![]() ,
,
所以直线![]() 的斜率为
的斜率为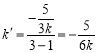 ,
,
故![]() ,为定值.
,为定值.

【题目】某市劳动部门坚持就业优先,采取多项措施加快发展新兴产业,服务经济,带来大量就业岗位,据政府工作报告显示,截至2018年末,全市城镇新增就业21.9万人,创历史新高.城镇登记失业率为4.2%,比上年度下降0.73个百分点,处于近20年来的最低水平.
(1)现从该城镇适龄人群中抽取100人,得到如下列联表:
失业 | 就业 | 合计 | |
男 | 3 | 62 | 65 |
女 | 2 | 33 | 35 |
合计 | 5 | 95 | 100 |
根据联表判断是否有99%的把握认为失业与性别有关?
附:
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
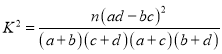
(2)调查显示,新增就业人群中,新兴业态,民营经济,大型国企对就业支撑作用不断增强,其岗位比例为![]() ,现从全市新增就业人群(数目较大)中抽取4人,记抽到的新兴业态的就业人数为X,求X的分布列和数学期望.
,现从全市新增就业人群(数目较大)中抽取4人,记抽到的新兴业态的就业人数为X,求X的分布列和数学期望.