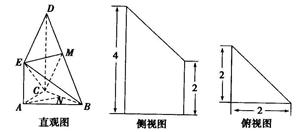
题目内容
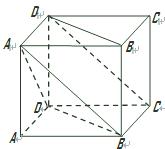
如图,在四棱柱ABCD-A1B1C1D1中,已知平面AA1C1C丄平面ABCD,且AB=BC=CA=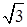 ,AD=CD=1.
,AD=CD=1.
 求证:BD⊥AA1;
求证:BD⊥AA1; 若四边形
若四边形 是菱形,且
是菱形,且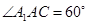 ,求四棱柱
,求四棱柱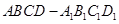 的体积.
的体积.
 详见解析;
详见解析;

解析试题分析: 在底面ABCD中,由各边的关系可知
在底面ABCD中,由各边的关系可知 再由面面垂直的性质定理可得
再由面面垂直的性质定理可得 平面
平面 ,从而证得BD⊥AA1;
,从而证得BD⊥AA1; 由于四棱柱底面各边及对角线CA长度都已知,故其面积容易求得.而易知四棱柱的高即菱形
由于四棱柱底面各边及对角线CA长度都已知,故其面积容易求得.而易知四棱柱的高即菱形 中AC边上的高,由
中AC边上的高,由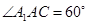 及
及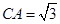 可得高
可得高 ,所以可得四棱柱体积V=
,所以可得四棱柱体积V= .
.
试题解析:(Ⅰ)在四边形 中,因为
中,因为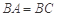 ,
, ,所以
,所以 2分
2分
又平面 平面
平面 ,且平面
,且平面 平面
平面
 平面
平面 ,所以
,所以 平面
平面 4分
4分
又因为 平面
平面 ,所以
,所以 . 6分
. 6分
(Ⅱ)过点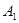 作
作 于点
于点 ,∵平面
,∵平面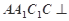 平面
平面

∴ 平面
平面
即 为四棱柱的一条高 8分
为四棱柱的一条高 8分
又∵四边形 是菱形,且
是菱形,且 ,
,
∴ 四棱柱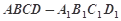 的高为
的高为 9分
9分
又∵ 四棱柱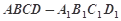 的底面面积
的底面面积 10分
10分
∴ 四棱柱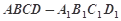 的体积为
的体积为 12分
12分
考点:1.面面垂直性质定理;2.棱柱的体积公式;3.解三角形.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 的球内有一个内接正方体(即正方体的顶点都在球面上).
的球内有一个内接正方体(即正方体的顶点都在球面上). 中,
中,
 底面
底面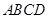 ,
,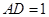 ,
,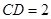 ,
,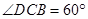 .
.
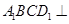 平面
平面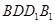 ;
;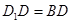 ,求四棱锥
,求四棱锥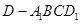 的体积.
的体积. 中,
中,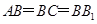 ,
, 为
为 的中点.
的中点.
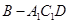 的体积.
的体积. ,在直角梯形
,在直角梯形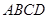 中,
中,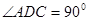 ,
,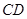 ∥
∥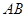 ,
, ,
,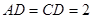 ,将
,将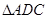 沿
沿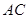 折起,使平面
折起,使平面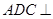 平面
平面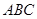 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
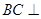 平面
平面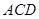 ;
; 的底面为直角梯形,
的底面为直角梯形,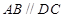 ,
,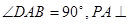 底面
底面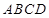 ,且
,且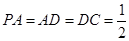 ,
,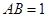 ,
,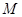 是
是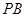 的中点。
的中点。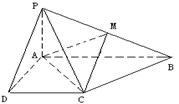
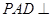 面
面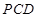 ;
;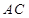 与
与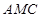 与面
与面 所成二面角的大小。
所成二面角的大小。 是边长为2的正方形,
是边长为2的正方形, ⊥平面
⊥平面 ,
, //
// 且
且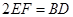 .
.
 ⊥平面
⊥平面 ;
; 的体积.
的体积.