题目内容
已知函数f(x)是定义在R上的奇函数,并且当x∈(0,+∞)时,f(x)=2x.
(1)求f(log2 )的值;
)的值;
(2)求f(x)的解析式.
(1)-3. (2) f(x)=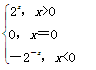 .
.
解析试题分析:(1)因为f(x)为奇函数,且当x∈(0,+∞)时,f(x)=2x,
所以f(log2 )=f(-log23)=-f(log23)=-2log23=-3. (6分)
)=f(-log23)=-f(log23)=-2log23=-3. (6分)
(2)设任意的x∈(-∞,0),则-x∈(0,+∞),
因为当x∈(0,+∞)时,f(x)=2x,所以f(-x)=2-x,
又因为f(x)是定义在R上的奇函数,则f(-x)=-f(x),
所以f(x)=-f(-x)=-2-x,即当x∈(-∞,0)时,f(x)=-2-x; (8分)
又因为f(0)=-f(0),所以f(0)=0, (10分)
综上可知,f(x)=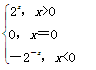 . (12分)
. (12分)
考点:本题主要考查分段函数的概念,函数的奇偶性,指数函数、对数函数的性质。
点评:典型题,奇函数在x=0处有意义,则有f(0)=0.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
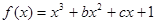 在区间
在区间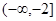 ,
,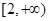 上单调递增,在区间[-2,2]上单调递减.
上单调递增,在区间[-2,2]上单调递减.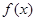 的解析式;
的解析式;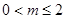 ,若对任意的x1、x2
,若对任意的x1、x2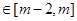 不等式
不等式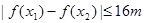 恒成立,求实数m的最小值。
恒成立,求实数m的最小值。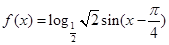 .
.
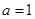 时,求函数
时,求函数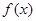 的极值;
的极值; 时,讨论函数
时,讨论函数 及任意
及任意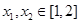 ,恒有
,恒有 成立,求实数
成立,求实数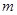 的取值范围.
的取值范围.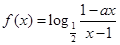 为奇函数,
为奇函数, 为常数.
为常数. 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;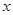 的值,不等式
的值,不等式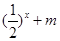 恒成立,求实数
恒成立,求实数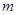 的取值范围.
的取值范围. 的函数
的函数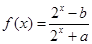 是奇函数.
是奇函数.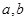 的值;
的值;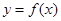 的单调性;
的单调性;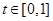 ,不等式
,不等式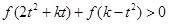 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.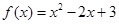
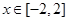 时,求
时,求 的值域
的值域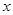 的不等式:
的不等式: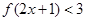
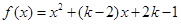 .
.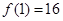 ,函数
,函数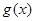 是R上的奇函数,当
是R上的奇函数,当 时
时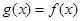 ,(i)求实数
,(i)求实数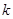 与
与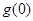
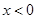 时,求
时,求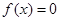 的两根中,一根属于区间
的两根中,一根属于区间 ,另一根属于区间
,另一根属于区间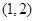 ,求实数
,求实数