题目内容
设函数
(Ⅰ) 当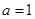 时,求函数
时,求函数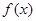 的极值;
的极值;
(Ⅱ)当 时,讨论函数
时,讨论函数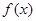 的单调性.
的单调性.
(Ⅲ)若对任意 及任意
及任意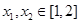 ,恒有
,恒有 成立,求实数
成立,求实数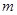 的取值范围.
的取值范围.
(Ⅰ) 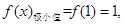 无极大值.
无极大值.
(Ⅱ)当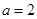 时,
时,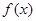 在
在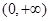 上是减函数;
上是减函数;
当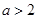 时,
时,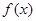 在
在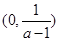 和
和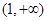 单调递减,在
单调递减,在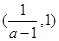 上单调递增;
上单调递增;
当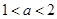 时,
时,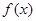 在
在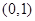 和
和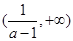 单调递减,在
单调递减,在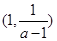 上单调递增;
上单调递增;
(Ⅲ)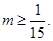
解析试题分析:(Ⅰ)函数的定义域为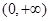 .
.
当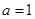 时,
时,
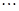 2分
2分
当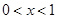 时,
时,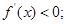 当
当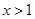 时,
时,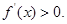
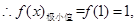 无极大值.
无极大值.  4分
4分
(Ⅱ)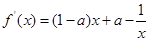
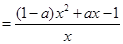
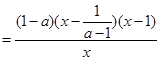
 5分
5分
当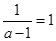 ,即
,即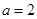 时,
时,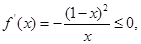
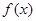 在定义域上是减函数;
在定义域上是减函数;
当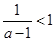 ,即
,即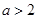 时,令
时,令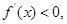 得
得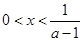 或
或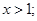
令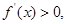 得
得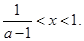 当
当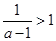 ,即
,即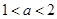 时,令
时,令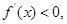 得
得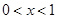 或
或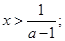
令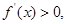 得
得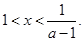 综上,当
综上,当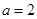 时,
时,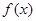 在
在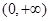 上是减函数;
上是减函数;
当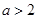 时,
时,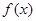 在
在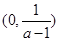 和
和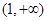 单调递减,在
单调递减,在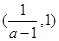 上单调递增;
上单调递增;
当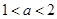 时,
时,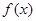 在
在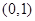 和
和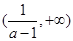 单调递减,在
单调递减,在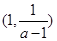 上单调递增;
上单调递增; 8分
8分
(Ⅲ)由(Ⅱ)知,当 时,
时,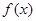 在
在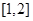 上单减,
上单减,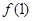 是最大值,
是最大值, 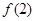 是最小值.
是最小值. 10分
10分 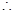
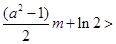
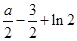
而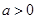 经整理得
经整理得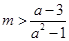 ,由
,由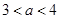 得
得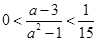 ,所以
,所以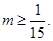 12分
12分
考点:本题主要考查应用导数研究函数的单调性、最值及不等式恒成立问题,不等式的解法。
点评:典型题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。涉及不等式恒成立问题,转化成了研究函数的最值之间的差,从而利用“分离参数法”又转化成函数的最值问题。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目


 的不等式
的不等式 
 的图象恒在函数
的图象恒在函数 的上方,求实数
的上方,求实数 的取值范围。
的取值范围。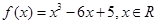
 的单调区间;
的单调区间; 的方程
的方程 有3个不同实根,求实数
有3个不同实根,求实数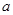 的取值范围;
的取值范围;
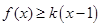 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -1.
-1.  时, 求函数f(x)的单调区间;
时, 求函数f(x)的单调区间;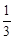 时, 设函数g(x)=x2-2bx-
时, 设函数g(x)=x2-2bx- , 若对于
, 若对于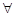 x1∈
x1∈ ,
,  [0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<
[0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e< +1).
+1). 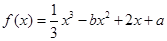 ,
,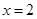 是
是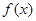 的一个极值点.
的一个极值点.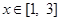 时,
时,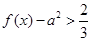 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.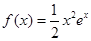 .
. )的值;
)的值;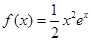 .
.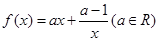 ,
, 。
。 与
与 的图象在x = x0处的切线斜率总想等,求x0的值;
的图象在x = x0处的切线斜率总想等,求x0的值; 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。