题目内容
8.存在最小的合数n,使得2n-1≡1(modn)成立,则n的值为( )| A. | 327 | B. | 341 | C. | 331 | D. | 355 |
分析 若2n-1 mod n=1,则2n-1-1 mod n=0,进而可得${2}^{\frac{n-1}{2}}-1$必为质数,即$\frac{n-1}{2}$为质数,逐一分析四个答案,可得结论.
解答 解:1 mod n=1恒成立,
若2n-1 mod n=1,则2n-1-1 mod n=0,
则n必为奇数,
则n-1为偶数,
故2n-1-1=(${2}^{\frac{n-1}{2}}+1$)(${2}^{\frac{n-1}{2}}-1$) mod n=0,
由n使满足2n-1≡1(modn)成立的最小合数,
则${2}^{\frac{n-1}{2}}-1$必为质数,则$\frac{n-1}{2}$为质数,
当n=327时,$\frac{n-1}{2}$=163是质数,满足条件;
当n=341时,$\frac{n-1}{2}$=170不是质数,不满足条件;
当n=331时,$\frac{n-1}{2}$=165不是质数,不满足条件;
当n=355时,$\frac{n-1}{2}$=177不是质数,不满足条件;
故选:A
点评 本题考查的知识点是同余与整除,其中正确理解${2}^{\frac{n-1}{2}}-1$必为质数,即$\frac{n-1}{2}$为质数,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知函数f(x)=$\left\{\begin{array}{l}{ax+a,x≥0}\\{{e}^{ax},x<0}\end{array}\right.$为R上的增函数,则实数a的取值范围是( )
| A. | (0,+∞) | B. | [1,+∞) | C. | (0,1] | D. | (1,+∞) |
20.设a=(lg3)2,b=30.3,c=lg$\sqrt{3}$,则( )
| A. | a<c<b | B. | c<a<b | C. | b<a<c | D. | b<c<a |
17.如果质点A按规律s=3t2运动,则在t=2时的瞬时速度是( )
| A. | 4 | B. | 6 | C. | 12 | D. | 24 |
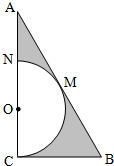 如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.
如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.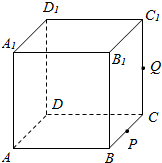 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}.时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}.时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$.