题目内容
设函数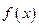 =
=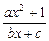 是奇函数,其中
是奇函数,其中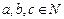 ,
,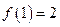 ,
,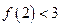 。
。
(Ⅰ)求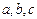 的值;
的值;
(Ⅱ)判断并证明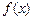 在
在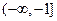 上的单调性。
上的单调性。
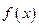 =
=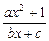 是奇函数,其中
是奇函数,其中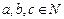 ,
,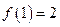 ,
,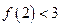 。
。(Ⅰ)求
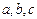 的值;
的值;(Ⅱ)判断并证明
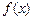 在
在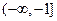 上的单调性。
上的单调性。(1)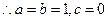 (2)见解析
(2)见解析
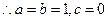 (2)见解析
(2)见解析(Ⅰ)由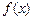 =
=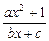 是奇函数得:
是奇函数得: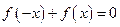
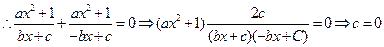 ,即
,即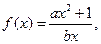
又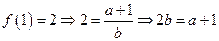
又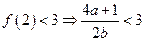
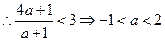 ,
,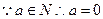 或1
或1
若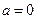 ,则
,则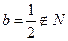 (舍去)
(舍去)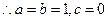
(Ⅱ)由(Ⅰ)知,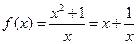 ,
, 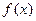 在
在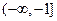 上单调递增。下用定义证明:设
上单调递增。下用定义证明:设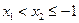 ,则:
,则:
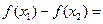
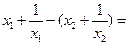
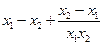
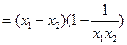 ,
,
因为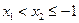 ,
,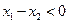 ,
,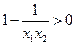

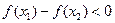 ,故
,故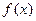 在
在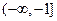 上单调递增。
上单调递增。
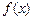 =
=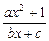 是奇函数得:
是奇函数得: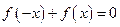
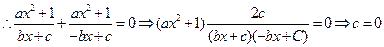 ,即
,即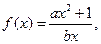
又
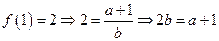
又
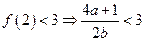
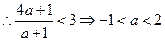 ,
,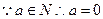 或1
或1若
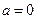 ,则
,则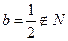 (舍去)
(舍去)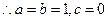
(Ⅱ)由(Ⅰ)知,
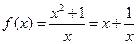 ,
, 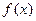 在
在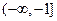 上单调递增。下用定义证明:设
上单调递增。下用定义证明:设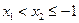 ,则:
,则: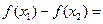
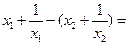
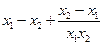
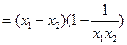 ,
,因为
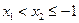 ,
,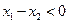 ,
,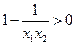

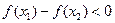 ,故
,故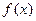 在
在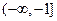 上单调递增。
上单调递增。
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 为
为 ,射线
,射线 为
为 ,动点
,动点 在
在 的内部,
的内部, 于
于 ,
, 于
于 ,四边形
,四边形 的面积恰为
的面积恰为 .
. 的纵坐标
的纵坐标 是横坐标
是横坐标 的函数,求这个函数
的函数,求这个函数 的解析式;
的解析式;
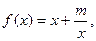 且函数
且函数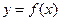 的图象经过点(1,2).
的图象经过点(1,2).  在(1,
在(1,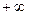 )上是增函数.
)上是增函数.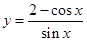 在点
在点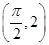 处的切线与直线
处的切线与直线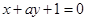 垂直,则
垂直,则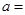
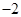
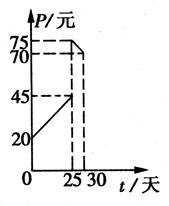
 10
10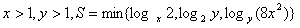 则S的最大值为 。
则S的最大值为 。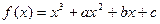 的图象过原点,且在x=1处取得极值,直线
的图象过原点,且在x=1处取得极值,直线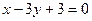 与曲线
与曲线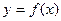 在原点处的切线互相垂直。
在原点处的切线互相垂直。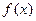 的解析式;
的解析式;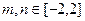 ,恒有
,恒有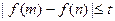 成立,求实数t的取值范围。
成立,求实数t的取值范围。 之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校. 已知船速为
之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校. 已知船速为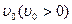 ,车速为
,车速为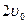 (水流速度忽略不计).
(水流速度忽略不计).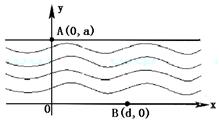
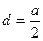 ,求该学生早晨上学时,从家出发到达学校所用的最短时间.
,求该学生早晨上学时,从家出发到达学校所用的最短时间. 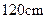 的正方形铁皮做一个无盖水箱,先在四角分别截去一个小正方形,然后把四边翻转
的正方形铁皮做一个无盖水箱,先在四角分别截去一个小正方形,然后把四边翻转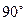 角,再焊接成水箱.问:水箱底边的长取多少时,水箱容积最大?最大容积是多少?
角,再焊接成水箱.问:水箱底边的长取多少时,水箱容积最大?最大容积是多少?