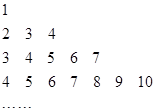题目内容
已知数列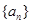 满足:
满足: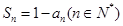 ,其中
,其中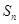 为数列
为数列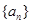 的前
的前 项和.
项和.
(1)试求数列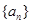 的通项公式;
的通项公式;
(2)设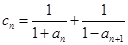 ,数列
,数列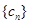 的前
的前 项和为
项和为 ,求证
,求证
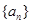 满足:
满足: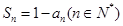 ,其中
,其中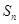 为数列
为数列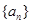 的前
的前 项和.
项和.(1)试求数列
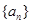 的通项公式;
的通项公式;(2)设
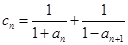 ,数列
,数列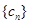 的前
的前 项和为
项和为 ,求证
,求证
解:(1)∵
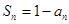 , ① ∴
, ① ∴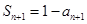 , ②
, ②②-①得
 ,∴
,∴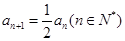 …………(4分)
…………(4分)又当
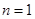 时,
时,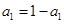 ,∴
,∴ ∴
∴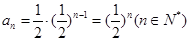 …………(6分)
…………(6分)(2)证明:∵
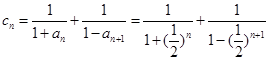
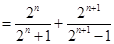
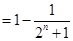
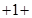
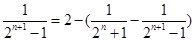 ………………………………(8分),
………………………………(8分), 又
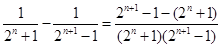 =
=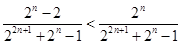
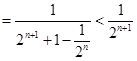
……………………(11分)
∴
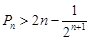 ∴
∴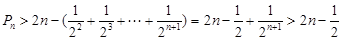 …………12分
…………12分略

练习册系列答案
相关题目
 满足
满足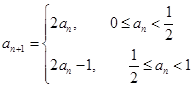 ,若
,若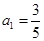 ,则数列的第2012项为( )
,则数列的第2012项为( )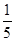
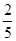
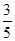
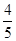
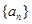 的前
的前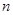 项和为
项和为 ,且
,且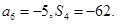
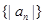 的前
的前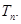
 ,
, ,其中
,其中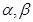 是方程
是方程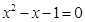 的两个根.
的两个根.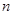 ,都有
,都有 ;
;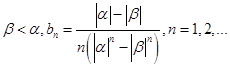 ,证明:
,证明: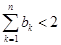 。
。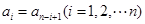 ,我们称
,我们称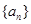 中,
中,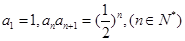
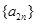 与
与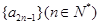 都是等比数列;
都是等比数列;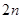 的和为
的和为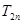 ,令
,令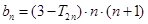 ,求数列
,求数列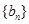 的最大项.
的最大项.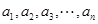 的前k项和为
的前k项和为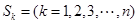 ,定义
,定义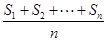 为该项数列的“凯森和”,如果项系数为99项的数列
为该项数列的“凯森和”,如果项系数为99项的数列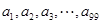 的“凯森和”为1000,那么项数为100的数列100,
的“凯森和”为1000,那么项数为100的数列100,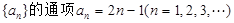 ,现将其中所有的完全平方数(即
,现将其中所有的完全平方数(即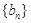 。
。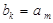 ,则正整数m关于正整数k的函数表达式为m= ;
,则正整数m关于正整数k的函数表达式为m= ; 能取到的最大值等于 。
能取到的最大值等于 。 从上而下,其中2012第一次出现在第 行,第 列.
从上而下,其中2012第一次出现在第 行,第 列.