题目内容
已知函数f(x)=
,函数g(x)=f2(x)+f(x)+t(t∈R).关于g(x)的零点,下列判断不正确的是( )
|
分析:由已知中函数f(x)=
的解析式,画出函数f(x)的图象,令m=f(x),可得m≥1时,m=f(x)有两根,m<1时,m=f(x)有一根,根据二次函数的图象和性质分析t取不同值时,g(x)=m2+m+t根的个数及分面情况,综合讨论结果,可得答案.
|
解答:解:函数f(x)=
的图象如下图所示:
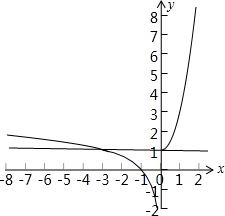
令m=f(x),m≥1时,m=f(x)有两根,m<1时,m=f(x)有一根,
若t=
,则g(x)=f2(x)+f(x)+
=[m+
]2=0
此时m=
,由上图可得,此时函数m=0有一个根,
即g(x)有一个零点,故A正确;
若t=-2,则g(x)=f2(x)+f(x)-2=(m+2)•(m-1)=0
此时m=-2,m=1,此时g(x)=0有三个根,
即g(x)有三个零点,故C正确;
若-2<t<
,则g(x)=m2+m+t=0有两个根,但均小于1
此时,g(x)=0有两个根,故B正确;
若t<-2,则g(x)=m2+m+t=0有两个根,一个大于1,一个小于1
此时,g(x)=0有三个根,故D错误;
故选D
|
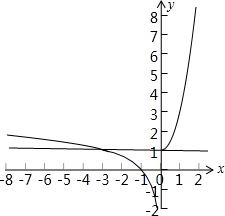
令m=f(x),m≥1时,m=f(x)有两根,m<1时,m=f(x)有一根,
若t=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
此时m=
| 1 |
| 2 |
即g(x)有一个零点,故A正确;
若t=-2,则g(x)=f2(x)+f(x)-2=(m+2)•(m-1)=0
此时m=-2,m=1,此时g(x)=0有三个根,
即g(x)有三个零点,故C正确;
若-2<t<
| 1 |
| 4 |
此时,g(x)=0有两个根,故B正确;
若t<-2,则g(x)=m2+m+t=0有两个根,一个大于1,一个小于1
此时,g(x)=0有三个根,故D错误;
故选D
点评:本题考查的知识点是根的存在性及根的个数判断,函数解析式的求解及常用方法,其中画出函数f(x)的图象,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目