函数y=2x-x2的图象大致是( ) A.B.C.D. 题目和参考答案——青夏教育精英家教网—

题目内容

函数y=2^x-x²的图象大致是（　　）

A、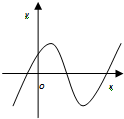

B、

C、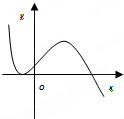

D、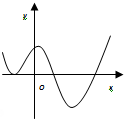

考点：函数的图象

专题：函数的性质及应用

分析：根据函数图象的交点的个数就是方程的解的个数，也就是y=0，图象与x轴的交点的个数，排除BC，再取特殊值，排除D

解答： 解：分别画出函数f（x）=2^x（红色曲线）和g（x）=x²（蓝色曲线）的图象，如图所示，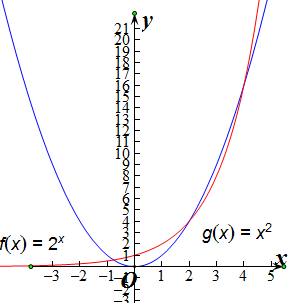

由图可知，f（x）与g（x）有3个交点，
所以y=2^x-x²=0，有3个解，
即函数y=2^x-x²的图象与x轴由三个交点，故排除B，C，
当x=-3时，y=2^-3-（-3）²＜0，故排除D
故选：A

点评：本题主要考查了函数图象的问题，关键是理解函数图象的交点和方程的解得个数的关系，排除是解决选择题的常用方法，属于中档题

练习册系列答案

相关题目

已知⊙O的两条弦AB与CD相互垂直，且交点为P，若

已知函数f（x）=sinx，g（x）=cos²x，以下判断正确的序号是

（1）函数h（x）=f（x）-tanx在x∈（-

，0]上的零点只有1个．
（2）函数h（x）=f（x+1）-

2x+2

在x∈（1，2π）上的零点只有1个．
（3）函数h（x）=

f（x）+g（x）+a在x∈[0，π]的零点个数为1个时，a无解
（4）函数h（x）=

f（x）+g（x）+a在x∈[0，π]的零点个数为2时，a∈（-1，-

）∪{-

}．

定义[x]表示不超过x的最大整数，若f（x）=cos（x-[x]），则下列结论中：
①y=f（x）为偶函数；
②y=f（x）为周期函数，周期为2π；
③y=f（x）的最小值为cos1，无最大值；
④y=f（x）无最小值，最大值为1．
正确的命题的个数为（　　）

在空间四边形ABCD中，E、F分别是AB、BC上的中点，G属于CD、H属于AD，EH与FG相交于点P，求证：交点P必在直线BD上．

设曲线y=x³-2x-2在P处的切线平行于直线x-y+3=0，则点P的坐标为

．

在平面直角坐标系xOy中，曲线y=x²-4x+3与坐标轴的交点都在圆C上．
（Ⅰ）求圆C的方程；
（Ⅱ）若圆C与直线x+y+m=0交于A，B两点，且

⊥

，求m的值．

试题分类