题目内容
设曲线y=x3-2x-2在P处的切线平行于直线x-y+3=0,则点P的坐标为 .
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,直线与圆
分析:设点P(m,n),求出函数的导数,求出切线的斜率,再由两直线平行的条件,得到方程,解得即可.
解答:
解:设点P(m,n),
y=x3-2x-2的导数y′=3x2-2,
即有在P处的切线斜率为:3m2-2,
由于在P处的切线平行于直线x-y+3=0,
则3m2-2=1,即得,m=1,
则n=m3-2m-2=1-2-2=-3,
则点P的坐标为(1,-3),
故答案为:(1,-3).
y=x3-2x-2的导数y′=3x2-2,
即有在P处的切线斜率为:3m2-2,
由于在P处的切线平行于直线x-y+3=0,
则3m2-2=1,即得,m=1,
则n=m3-2m-2=1-2-2=-3,
则点P的坐标为(1,-3),
故答案为:(1,-3).
点评:本题考查导数的几何意义:曲线在该点处切线的斜率,考查两直线平行的条件,考查运算能力,属于基础题.

练习册系列答案
相关题目
函数y=2x-x2的图象大致是( )
A、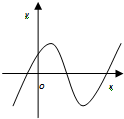 |
B、 |
C、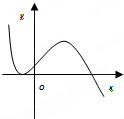 |
D、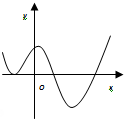 |
设a,b是不同的直线,α,β是不同的平面,则下列结论错误的是( )
| A、若a⊥α,b∥α,则a⊥b |
| B、若a⊥α,b⊥α,则a∥b |
| C、若b∥α,b?β,则α∥β |
| D、若a⊥α,a⊥β,则α∥β |
如图,Rt△O′A′B′是一平面图形的直观图,斜边O′B′=2,则这个平面图形的面积是( )

A、
| ||||
| B、1 | ||||
C、
| ||||
D、2
|