题目内容
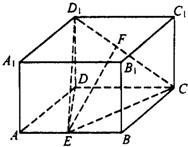 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.E、F分别为线段AB、D1C上的点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.E、F分别为线段AB、D1C上的点.(Ⅰ)若E、F分别为线段AB、D1C的中点,求证:EF∥平面AD1;
(Ⅱ)已知二面角D1-EC-D的大小为
| π | 6 |
分析:(Ⅰ)欲证EF∥平面AD1,可利用平面EFG∥平面AD1进行证明,取DC的中点G,连接FG,GE,而FG∥DD1,DD1?平面AD1,根据线面平行的判定定理可知FG∥平面AD1,同理可证GE∥平面AD1,且FG∩GE=G,从而平面EFG∥平面AD1,EF?平面EFG,根据面面平行的性质可知EF∥平面AD1;
(Ⅱ)根据D1D⊥平面ABCD,过D在平面ABCD内作DH⊥EC于H,连接D1H,而DH是D1H在平面ABCD内的射影,则∠DHD1为二面角D1-EC-D的平面角,在△DHD1中,根据tan∠DHD1值求出DH,根据面积求出EC,最后根据EC2=1+EB2求出所求即可.
(Ⅱ)根据D1D⊥平面ABCD,过D在平面ABCD内作DH⊥EC于H,连接D1H,而DH是D1H在平面ABCD内的射影,则∠DHD1为二面角D1-EC-D的平面角,在△DHD1中,根据tan∠DHD1值求出DH,根据面积求出EC,最后根据EC2=1+EB2求出所求即可.
解答:解:(Ⅰ)证明:取DC的中点G,连接FG,GE.
∵FG∥DD1,DD1?平面AD1,
∴FG∥平面AD1.
同理:GE∥平面AD1,且FG∩GE=G,
∴平面EFG∥平面AD1,EF?平面EFG,
∴EF∥平面AD1.
(Ⅱ)D1D⊥平面ABCD,过D在平面ABCD内作DH⊥EC于H,连接D1H.
∵DH是D1H在平面ABCD内的射影,
∴D1H⊥EC.
∴∠DHD1为二面角D1-EC-D的平面角.
即∠DHD1=
.
在△DHD1中,tan∠DHD1=
,
∴DH=
,S△DEC=
×2×1=
×EC×
,
∴EC=
,
∴EC2=1+EB2,
∴EB=
,
∴AE=2-
.
∵FG∥DD1,DD1?平面AD1,
∴FG∥平面AD1.
同理:GE∥平面AD1,且FG∩GE=G,
∴平面EFG∥平面AD1,EF?平面EFG,
∴EF∥平面AD1.
(Ⅱ)D1D⊥平面ABCD,过D在平面ABCD内作DH⊥EC于H,连接D1H.
∵DH是D1H在平面ABCD内的射影,
∴D1H⊥EC.
∴∠DHD1为二面角D1-EC-D的平面角.
即∠DHD1=
| π |
| 6 |
在△DHD1中,tan∠DHD1=
| ||
| 3 |
∴DH=
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴EC=
2
| ||
| 3 |
∴EC2=1+EB2,
∴EB=
| ||
| 3 |
∴AE=2-
| ||
| 3 |
点评:本题主要考查了平面与平面平行的判定,以及与二面角有关的立体几何综合题,同时考查了空间想象能力、分析推理能力,属于中档题.

练习册系列答案
相关题目
 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )

 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.