题目内容
16.已知关于x的不等式kx2-2x+6k<0,(k>0)若不等式的解集为集合{x|2<x<3}的子集,求实数k的取值范围.分析 设f(x)=kx2-2x+6k,原问题等价于原问题等价于△≤0或$\left\{\begin{array}{l}{f(2)≥0}\\{f(3)≥0}\\{2≤\frac{1}{k}≤3}\end{array}\right.$,由此求出k的取值范围
解答 解∵不等式对应的方程kx2-2x+6k=0的判别式为
△=4-24k2,
设f(x)=kx2-2x+6k,
则原问题等价于△≤0或$\left\{\begin{array}{l}{f(2)≥0}\\{f(3)≥0}\\{2≤\frac{1}{k}≤3}\end{array}\right.$;
由△≤0,即4-24k2≤0,
解得k≤-$\frac{\sqrt{6}}{6}$或k≥$\frac{\sqrt{6}}{6}$,
又∵k>0,∴k≥$\frac{\sqrt{6}}{6}$;
由$\left\{\begin{array}{l}{f(2)≥0}\\{f(3)≥0}\\{2≤\frac{1}{k}≤3}\end{array}\right.$,
即$\left\{\begin{array}{l}{10k-4≥0}\\{15k-6≥0}\\{2≤\frac{1}{k}≤3}\end{array}\right.$,
解得$\frac{2}{5}$≤k≤$\frac{1}{2}$;
综上,符合条件的k的取值范围是[$\frac{2}{5}$,+∞).
点评 本题考查了含有字母系数的不等式的解法与应用问题,也考查了不等式的恒成立问题,解题时应对字母系数进行分析、讨论,是中档题.

练习册系列答案
相关题目
6.已知△ABC的三边a,b,c所对的角分别为A,B,C,若a:b:c=7:5:3.则∠A等于( )
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
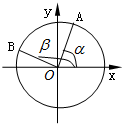 如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.
如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.