题目内容
11．
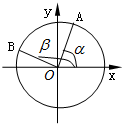如图，在平面直角坐标系xoy中，以ox轴为始边作一个锐角α和一个钝角β，它们的终边分别与单位圆相交于点A和点B．且点A的坐标为$（\frac{{\sqrt{5}}}{5}，\frac{{2\sqrt{5}}}{5}）$，点B的坐标为$（-\frac{{3\sqrt{10}}}{10}，\frac{{\sqrt{10}}}{10}）$．（1）求sinα，cosα，tanα的值；
（2）求tan（α+β）的值及α+β的值．
分析 （1）由题意和三角函数的定义可得；（2）同（1）可得tanβ，由两角和的正切可得tan（α+β），结合角的范围可得α+β
解答 解：（1）由题意和三角函数的定义可得sinα=$\frac{2\sqrt{5}}{5}$，cosα=$\frac{\sqrt{5}}{5}$，tanα=2；
（2）同（1）可得sinβ=$\frac{\sqrt{10}}{10}$，cosβ=-$\frac{3\sqrt{10}}{10}$，tanβ=-$\frac{1}{3}$，
∴tan（α+β）=$\frac{tanα+tanβ}{1-tanαtanβ}$=1，结合α为锐角β为钝角可得α+β=$\frac{5π}{4}$
点评 本题考查两角和与差的三角函数公式，涉及三角函数的定义，属基础题．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，抛物线y=ax2+bx-4与x轴交于点A（-2，0）和点B，与y轴交于点C，直线x=1是该抛物线的对称轴．