题目内容
本小题满分14分)
设函数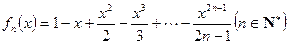 .
.
(Ⅰ)研究函数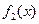 的单调性;
的单调性;
(Ⅱ)判断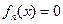 的实数解的个数,并加以证明.
的实数解的个数,并加以证明.
设函数
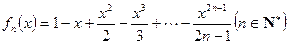 .
.(Ⅰ)研究函数
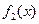 的单调性;
的单调性;(Ⅱ)判断
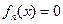 的实数解的个数,并加以证明.
的实数解的个数,并加以证明.解:(Ⅰ)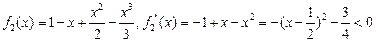 ,
,
所以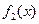 在
在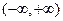 单调递减. ………………………………………(4分)
单调递减. ………………………………………(4分)
(Ⅱ)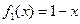 有唯一实数解
有唯一实数解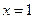 .…………………………………(6分)
.…………………………………(6分)
当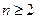 时,由
时,由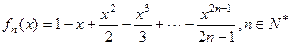 ,得
,得
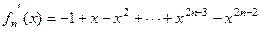 .
.
(1)若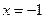 ,则
,则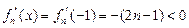 .
.
(2) 若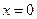 ,则
,则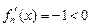 .
.
(3) 若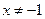 且
且 时,则
时,则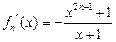 .
.
①当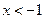 时,
时,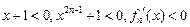 .
.
②当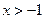 时,
时,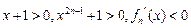 .
.
综合(1),(2), (3),得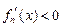 ,即
,即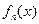 在
在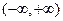 单调递减.
单调递减.
又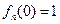 >0,
>0,

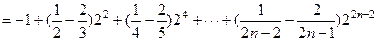
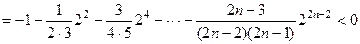 ,
,
所以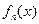 在
在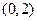 有唯一实数解,从而
有唯一实数解,从而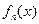 在
在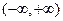 有唯一实数解.
有唯一实数解.
综上,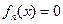 有唯一实数解. ………………………………………………(14分)
有唯一实数解. ………………………………………………(14分)
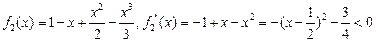 ,
,所以
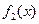 在
在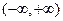 单调递减. ………………………………………(4分)
单调递减. ………………………………………(4分)(Ⅱ)
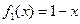 有唯一实数解
有唯一实数解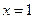 .…………………………………(6分)
.…………………………………(6分)当
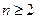 时,由
时,由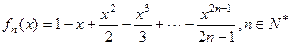 ,得
,得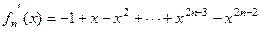 .
.(1)若
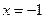 ,则
,则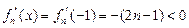 .
.(2) 若
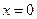 ,则
,则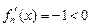 .
.(3) 若
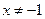 且
且 时,则
时,则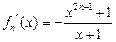 .
.①当
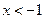 时,
时,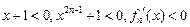 .
.②当
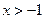 时,
时,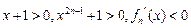 .
.综合(1),(2), (3),得
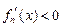 ,即
,即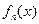 在
在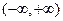 单调递减.
单调递减.又
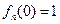 >0,
>0,
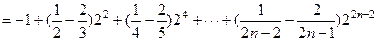
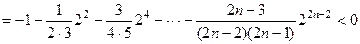 ,
,所以
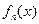 在
在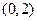 有唯一实数解,从而
有唯一实数解,从而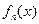 在
在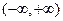 有唯一实数解.
有唯一实数解.综上,
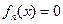 有唯一实数解. ………………………………………………(14分)
有唯一实数解. ………………………………………………(14分)略

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
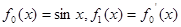 ,
,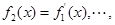
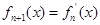 ,n∈N,则
,n∈N,则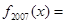 ( )
( )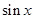
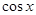
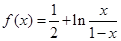 .
.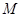 ,使得函数
,使得函数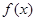 图象上任意一点
图象上任意一点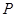 关于
关于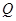 也在函数
也在函数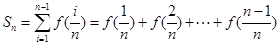 ,其中
,其中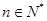 且
且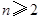 ,求
,求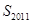 ;
;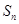 ,求证:对于任意
,求证:对于任意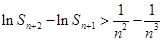 .
.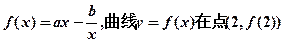 处的切线方程为
处的切线方程为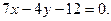
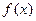 的解析式;
的解析式;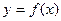 上任一
上任一 点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值. 在点
在点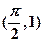 处的切线斜率为 ▲ .
处的切线斜率为 ▲ . 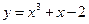 上一点P的切线与直线平行
上一点P的切线与直线平行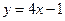 ,则切点的坐标为 。
,则切点的坐标为 。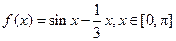 ,
,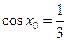 (
(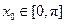 ).那么下面命题中真命题的序号是
).那么下面命题中真命题的序号是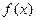 的最大值为
的最大值为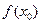 ②
② 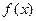 在
在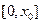 上是减函数 ④
上是减函数 ④ 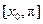 上是减函数
上是减函数 ②④
②④