题目内容
6.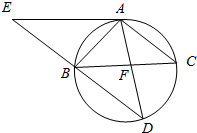 如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5.
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5.(1)求证:四边形AEBC为平行四边形.
(2)求线段CF的长.
分析 (1)由已知条件推导出∠ABC=∠BAE,从而得到AE∥BC,再由BD∥AC,能够证明四边形ACBE为平行四边形.
(2)由已知条件利用切割线定理求出EB=4,由此能够求出CF=$\frac{8}{3}$.
解答 (1)证明:∵AE与圆相切于点A,∴∠BAE=∠ACB,
∵AB=AC,∴∠ABC=∠ACB,∴∠ABC=∠BAE,
∴AE∥BC,
∵BD∥AC,∴四边形ACBE为平行四边形.
(2)解:∵AE与圆相切于点A,
∴AE2=EB•(EB+BD),即62=EB•(EB+5),
解得EB=4,
根据(1)有AC=EB=4,BC=AE=6,
设CF=x,由BD∥AC,得$\frac{AC}{BD}=\frac{CF}{BF}$,
∴$\frac{4}{5}=\frac{x}{6-x}$,解得x=$\frac{8}{3}$,
∴CF=$\frac{8}{3}$.
点评 本题考查平行四边形的证明,考查线段长的求法,是中档题,解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
相关题目
16.已知i是虚数单位,则复数$\frac{1-2i}{1+2i}$=( )
| A. | -$\frac{3}{5}$-$\frac{4}{5}$i | B. | -$\frac{3}{5}$+$\frac{4}{5}$i | C. | $\frac{3}{5}$-$\frac{4}{5}$i | D. | $\frac{3}{5}$+$\frac{4}{5}$i |
16.已知点C在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,以C为圆心的圆与x轴相切于椭圆的右焦点F,若圆C与y轴相切,则椭圆的离心率为( )
| A. | $\sqrt{2}$-1 | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\sqrt{3}$-1 |
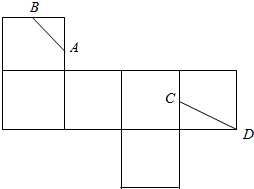 如图是一个正方体的平面展开图,A,B,C均为所在棱的中点,D为正方体的顶点,若正方体的棱长为2,则在正方体中,封闭折线ABCDA的长为3$\sqrt{2}+\sqrt{5}$.
如图是一个正方体的平面展开图,A,B,C均为所在棱的中点,D为正方体的顶点,若正方体的棱长为2,则在正方体中,封闭折线ABCDA的长为3$\sqrt{2}+\sqrt{5}$.