题目内容
13.设F1、F2分别为椭圆$\frac{{x}^{2}}{4}$+y2=1的左、右焦点,点P在椭圆上,且|$\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$|=2$\sqrt{3}$,则∠F1PF2=( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 由题意方程求得焦距,利用平面向量的减法运算得到$\overrightarrow{P{F}_{1}}-\overrightarrow{P{F}_{2}}=\overrightarrow{{F}_{2}{F}_{1}}$,与已知|$\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$|=2$\sqrt{3}$同时两边平方后可得$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=0$,由此可得答案.
解答 解:如图,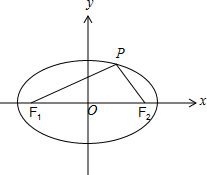
由椭圆$\frac{{x}^{2}}{4}$+y2=1,得a=2,b=1,c=$\sqrt{3}$,
$\overrightarrow{P{F}_{1}}-\overrightarrow{P{F}_{2}}=\overrightarrow{{F}_{2}{F}_{1}}$,则$(\overrightarrow{P{F}_{1}}-\overrightarrow{P{F}_{2}})^{2}={\overrightarrow{{F}_{2}{F}_{1}}}^{2}$,
即$|\overrightarrow{P{F}_{1}}{|}^{2}-2\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}+|\overrightarrow{P{F}_{2}}{|}^{2}=|\overrightarrow{{F}_{1}{F}_{2}}{|}^{2}$=12,
由|$\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$|=2$\sqrt{3}$,得$|\overrightarrow{P{F}_{1}}{|}^{2}+2\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}+|\overrightarrow{P{F}_{2}}{|}^{2}=12$,
∴$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=0$,即$\overrightarrow{P{F}_{1}}⊥\overrightarrow{P{F}_{2}}$,
∴∠F1PF2=$\frac{π}{2}$.
故选:D.
点评 本题考查了椭圆的简单性质,考查了平面向量的数量积运算,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 An(n∈N)系列的纸张规格如图,其特点是
An(n∈N)系列的纸张规格如图,其特点是①A0,A1,A2,…An所有规格的纸张的长宽比都相同;
②A0对裁后可以得到两张A1,A1对裁后可以得到两张A2,…,An-1对裁后可以得到两张An;
若梅平方厘米重量为b克的A0,A1,A2,…An纸张各一张,其中A4纸较短边的长为a厘米,记这(n+1)纸张的重量之和为Sn+1,则下列论断错误的是( )
| A. | 存在n∈N,使得Sn+1=32$\sqrt{2}$a2b | B. | 存在n∈N,使得Sn+1=16$\sqrt{2}$a2b | ||
| C. | 对于任意n∈N,使得Sn+1≤32$\sqrt{2}$a2b | D. | 对于任意n∈N,使得Sn+1≥16$\sqrt{2}$a2b |
| A. | 1:6 | B. | 1:5 | C. | 1:4 | D. | 1:3 |
| A. | ∅ | B. | {x|0<x<1} | C. | {x|x<0} | D. | {x|x>1} |
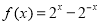 ,数列
,数列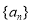 满足
满足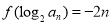 .
.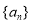 的通项公式;
的通项公式;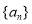 是递减数列.
是递减数列.