题目内容
【题目】设
、
、
是集合，称
为有序三元组，如果集合、、满足
，且
，则称有序三元组为最小相交（其中
表示集合
中的元素个数），如集合
，
，
就是最小相交有序三元组，则由集合
的子集构成的最小相交有序三元组的个数是________
【答案】7680
【解析】
令S={1，2，3，4，5，6}，由题意知，必存在两两不同的x，y，z∈S，使得A∩B={x}，B∩C={y}，C∩A={z}，而要确定x，y，z共有6×5×4种方法；对S中剩下的3个元素，每个元素有4种分配方式，即可得到最小相交的有序三元组（A，B，C）的个数．
令S={1，2，3，4，5，6}，如果（A，B，C）是由S的子集构成的最小相交的有序三元组，则存在两两不同的x，y，z∈S，使得A∩B={x}，B∩C={y}，C∩A={z}，（如图），要确定x，y，z共有6×5×4种方法；
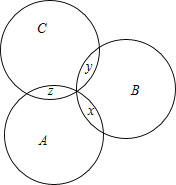
对S中剩下的3个元素，每个元素有4种分配方式，即它属于集合A，B，C中的某一个或不属于任何一个，则有43种确定方法．
所以最小相交的有序三元组（A，B，C）的个数6×5×4×43=7680．
故答案为：7680
练习册系列答案
相关题目
