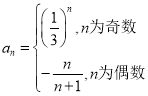Question

【题目】在三棱锥A-BCD中，平面ABC丄平面ADC, AD丄AC,AD=AC, ，若此三棱锥的外接球表面积为，则三棱锥A-BCD体积的最大值为（ ）

A.7B.12C.6D.

Answer 1

【答案】C

【解析】

设三棱锥A﹣BCD外接球的半径为R，三棱锥的外接球球心为O，△ABC的外心为O1，△ABC的外接圆半径为r，取DC的中点为O2，过O2作O2E⊥AC，则OO1⊥平面ABC，OO2⊥平面ADC，连结OA，O1A，则O1A＝r，设AD＝AC＝b，则OO1＝O2Eb，由S＝4πR2＝28π，解得R，由正弦正理求出b，若三棱锥A﹣BCD的体积最大，则只需△ABC的面积最大，由此能求出三棱锥A﹣BCD的体积的最大值．

根据题意，设三棱锥A﹣BCD外接球的半径为R，

三棱锥的外接球球心为O，

△ABC的外心为O1，△ABC的外接圆半径为r，

取DC的中点为O2，过O2作O2E⊥AC，

则OO1⊥平面ABC，OO2⊥平面ADC，

如图，连结OA，O1A，则O1A＝r，

设AD＝AC＝b，则OO1＝O2Eb，

由S＝4πR2＝28π，解得R，

在△ABC中，由正弦正理得2r，

∴2r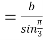，解得b，

在Rt△OAO1中，7＝r2+（）2，解得r＝2，b＝2，∴AC＝2，

若三棱锥A﹣BCD的体积最大，则只需△ABC的面积最大，

在△ABC中，AC2＝AB2+BC2﹣2ABBCcos∠ABC，

∴12＝AB2+BC2﹣ABBC≥2ABBC﹣ABBC，

解得ABBC≤12，

∴3，

∴三棱锥A﹣BCD的体积的最大值：

6．

故选：C．