题目内容
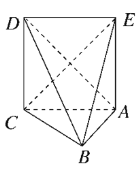
【题目】如图，在三棱锥D－ABC中，
底面ABC，
为正三角形，若
，
，则三棱锥D－ABC与三棱锥E－ABC的公共部分构成的几何体的外接球的体积为（ ）
A.
B.
C.
D.
【答案】B
【解析】
已知条件说明
是正方形，记
与
的交点为
，则
是等腰直角三角形，
是斜边
的中点，是的外心，
平面
，设
是
的外心，即
，则是
的外接球的球心，由此可得球的半径，从而得球的体积．
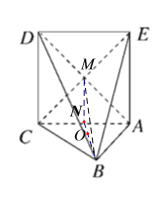
如图，设与的交点为，三棱锥是三棱锥D－ABC与三棱锥E－ABC的公共部分．
设是中点，连接
，在
上，且，∵
是正三角形，∴是的外心．
由
底面ABC，得
，又
，∴是正方形，∴
，即是等腰直角三角形，是的外心．
∵底面ABC，
底面ABC，∴
，
是正三角形，是中点，∴
，
，∴平面，即平面
，∵是的外心，∴是的外接球的球心，
其半径为
，球体积为
．
故选：B．
备战中考寒假系列答案
【题目】进入12月以来，某地区为了防止出现重污染天气，坚持保民生、保蓝天，严格落实机动车限行等一系列“管控令”.该地区交通管理部门为了了解市民对“单双号限行”的赞同情况，随机采访了220名市民，将他们的意见和是否拥有私家车情况进行了统计，得到如下的
列联表：
赞同限行 | 不赞同限行 | 合计 | |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
（1）根据上面的列联表判断，能否在犯错误的概率不超过0.001的前提下认为“是否赞同限行与是否拥有私家车”有关；
（2）为了了解限行之后是否对交通拥堵、环境污染起到改善作用，从上述调查的不赞同限行的人员中按分层抽样抽取6人，再从这6人中随机抽出3名进行电话回访，求3人中至少抽到1名“没有私家车”人员的概率.
附：
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】大连市某企业为确定下一年投入某种产品的宣传费，需了解年宣传费
（单位：千元）对年销售量
（单位：
）和年利润
（单位：千元）的影响，对近8年的年宣传费
和年销售量
数据作了初步处理，得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 573 | 6.8 | 289.8 | 1.6 | 215083.4 | 31280 |
表中
，
.
与
哪一个适宜作为年销售量关于年宣传费的回归方程类型？（给出判断即可，不必说明理由）
根据
的判断结果及表中数据，建立关于的回归方程；
已知这种产品的年利润与、的关系为
.根据的结果回答下列问题：
年宣传费
时，年销售量及年利润的预报值是多少？
年宣传费为何值时，年利润的预报值最大？
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
.
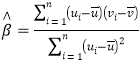