题目内容
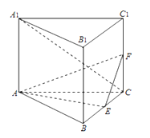
【题目】如图,已知椭圆![]() ,
,![]() 为椭圆的左右顶点,焦点
为椭圆的左右顶点,焦点![]() 到短轴端点的距离为2,且
到短轴端点的距离为2,且![]() ,
,![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的两点,直线
的两点,直线![]() 的斜率等于直线
的斜率等于直线![]() 斜率的2倍.
斜率的2倍.
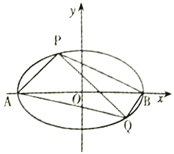
(1)求直线![]() 与直线
与直线![]() 的斜率乘积值;
的斜率乘积值;
(2)求证:直线![]() 过定点,并求出该定点;
过定点,并求出该定点;
(3)求三角形![]() 的面积
的面积![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)证明见解析,定点为
;(2)证明见解析,定点为![]() ;(3)
;(3)![]()
【解析】
(1)由题意可得:a=2,![]() ,a2=b2+c2,联立解出可得椭圆E的方程为:
,a2=b2+c2,联立解出可得椭圆E的方程为:![]() 1.设P点坐标(x,y),y2
1.设P点坐标(x,y),y2![]() (4﹣x2),则A(﹣2,0),B(2,0),利用斜率计算公式可得kAPkBP
(4﹣x2),则A(﹣2,0),B(2,0),利用斜率计算公式可得kAPkBP![]() ,由kBQ=2kAP,可得kBPkBQ.
,由kBQ=2kAP,可得kBPkBQ.
(2)当直线PQ的斜率存在时,设lPQ:y=kx+t与x轴的交点为M,与椭圆方程联立得:(2k2+1)x2+4ktx+2t2﹣4=0,设P(x1,y1),Q(x2,y2),由kBPkBQ=﹣1,即![]() 0,利用数量积运算性质、根与系数的关系可得结论.
0,利用数量积运算性质、根与系数的关系可得结论.
(3)由(2)可知: t![]() .且S=S△APQ=S△APM+S△AQM
.且S=S△APQ=S△APM+S△AQM![]() |y1﹣y2|
|y1﹣y2|![]() ,利用根与系数的关系、函数的单调性可得S
,利用根与系数的关系、函数的单调性可得S![]() .当直线PQ的斜率不存在时,可得|PQ|
.当直线PQ的斜率不存在时,可得|PQ|![]() ,可得S.
,可得S.
(1)解:由题意可得:a=2,![]() ,a2=b2+c2,
,a2=b2+c2,
联立解得a=2,b=c![]() .
.
∴椭圆E的方程为:![]() 1.
1.
设P点坐标(x,y),y2![]() (4﹣x
(4﹣x
kAP![]() ,kBP
,kBP![]() ,
,
则kAPkBP![]() ,
,
由kBQ=2kAP,故kBPkBQ=﹣1.
∴直线BP与直线BQ的斜率乘积为﹣1为定值.
(2)证明:当直线PQ的斜率存在时,设lPQ:y=kx+t与x轴的交点为M,联立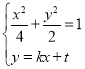 ,
,
整理得:(2k2+1)x2+4ktx+2t2﹣4=0,
设P(x1,y1),Q(x2,y2),则x1+x2![]() ,x1x2
,x1x2![]() ,
,
由kBPkBQ=﹣1,即![]() 0,则y1y2+x1x2﹣2(x1+x2)+4=0,
0,则y1y2+x1x2﹣2(x1+x2)+4=0,
得(k2+1)x1x2+(kt﹣2)(x1+x2)+4+t2=0,
4k2+8kt+3t2=0,得t=﹣2k或t![]() k.y=k(x﹣2)或y=k(x
k.y=k(x﹣2)或y=k(x![]() ),
),
所以过定点(2,0)或(![]() ,0),
,0),
A(2,0)为椭圆的右顶点,舍去,
当直线PQ的斜率不存在时,当![]() 时易得
时易得![]() ,满足
,满足![]() 0
0
综上直线PQ过定点M(![]() ,0).
,0).
(3)解:由(2)可知:当直线PQ的斜率存在时,t![]()
S=S△APQ=S△APM+S△AQM![]() |y1﹣y2|
|y1﹣y2|![]()
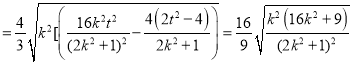 ,令
,令![]() m∈(0,1),则S
m∈(0,1),则S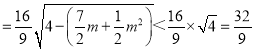 ,
,
当直线PQ的斜率不存在时,由(2)|PQ|![]() ,可得S
,可得S![]() .
.
综上可得:当PQ⊥x轴时,三角形APQ的面积S取得最大值![]() .
.

 高中必刷题系列答案
高中必刷题系列答案【题目】为了响应国家号召,某校组织部分学生参与了“垃圾分类,从我做起”的知识问卷作答,并将学生的作答结果分为“合格”与“不合格”两类与“问卷的结果”有关?
不合格 | 合格 | |
男生 | 14 | 16 |
女生 | 10 | 20 |
(1)是否有90%以上的把握认为“性别”与“问卷的结果”有关?
(2)在成绩合格的学生中,利用性别进行分层抽样,共选取9人进行座谈,再从这9人中随机抽取5人发送奖品,记拿到奖品的男生人数为X,求X的分布列及数学期望![]() .
.
附: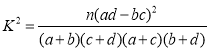
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.703 | 3.841 | 6.635 | 10.828 |