题目内容
(本小题满分12分)在平面直角坐标系中,已知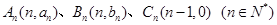 ,满足向量
,满足向量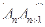 与向量
与向量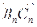 共线,且点
共线,且点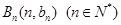 都在斜率为6的同一条直线上。若
都在斜率为6的同一条直线上。若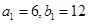 。求(1)数列
。求(1)数列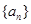 的通项
的通项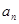 (2)数列{
(2)数列{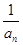 }的前n项和
}的前n项和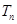
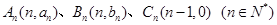 ,满足向量
,满足向量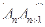 与向量
与向量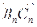 共线,且点
共线,且点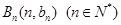 都在斜率为6的同一条直线上。若
都在斜率为6的同一条直线上。若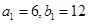 。求(1)数列
。求(1)数列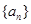 的通项
的通项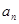 (2)数列{
(2)数列{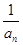 }的前n项和
}的前n项和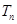
(1) an=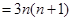 .(2)
.(2) 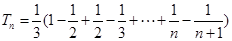
 。
。
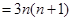 .(2)
.(2) 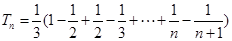
 。
。本试题主要是考查了数列的通项公式,以及数列的前n项和的求解问题。
(1)点Bn(n,bn)(n∈N*)都在斜率为6的同一条直线上,可以得到bn+1-bn=6,,进而求解通项公式。然后利用关系式,求解数列an
(2)在第一问的基础上,裂项求和得到结论。
解:(1)∵点Bn(n,bn)(n∈N*)都在斜率为6的同一条直线上, ∴
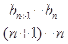 =6,
=6,
即bn+1-bn="6," ………2分
于是数列{bn}是等差数列,故bn="12+6(n-1)" =6n+6. ………4分
∵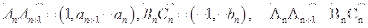 共线.
共线.
∴1×(-bn)-(-1)(an+1-an )=0,即an+1-an=bn ………6分
∴当n≥2时,an=a1+(a2-a1)+(a3-a2)+ …+(an-an-1)=a1+b1+b2+b3+…+bn-1
=a1+b1(n-1)+3(n-1)(n-2)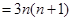 ………8分
………8分
当n=1时,上式也成立。 所以an=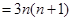 . ………9分
. ………9分
(2)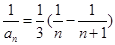
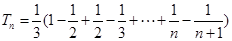
 ………12分
………12分
(1)点Bn(n,bn)(n∈N*)都在斜率为6的同一条直线上,可以得到bn+1-bn=6,,进而求解通项公式。然后利用关系式,求解数列an
(2)在第一问的基础上,裂项求和得到结论。
解:(1)∵点Bn(n,bn)(n∈N*)都在斜率为6的同一条直线上, ∴

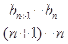 =6,
=6,即bn+1-bn="6," ………2分
于是数列{bn}是等差数列,故bn="12+6(n-1)" =6n+6. ………4分
∵
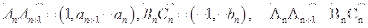 共线.
共线.∴1×(-bn)-(-1)(an+1-an )=0,即an+1-an=bn ………6分
∴当n≥2时,an=a1+(a2-a1)+(a3-a2)+ …+(an-an-1)=a1+b1+b2+b3+…+bn-1
=a1+b1(n-1)+3(n-1)(n-2)
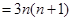 ………8分
………8分当n=1时,上式也成立。 所以an=
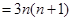 . ………9分
. ………9分 (2)
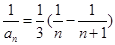
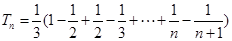
 ………12分
………12分
练习册系列答案
相关题目
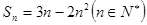 ,则当n>2时,下列不等式中的是( )
,则当n>2时,下列不等式中的是( )



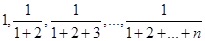 的前
的前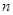 项和为__________
项和为__________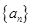 满足
满足 ,
, (
(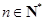 ),则
),则 的值为 .
的值为 .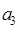 成等差数列.
成等差数列.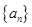 满足
满足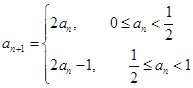 ,若
,若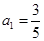 ,则数列的第2012项为( )
,则数列的第2012项为( )



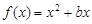 的图象在点
的图象在点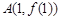 处的切线
处的切线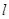 与直线
与直线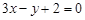 平行,若数
平行,若数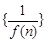 的前
的前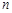 项和为
项和为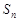 ,则
,则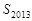 的值为 .
的值为 . 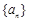 的前n项和
的前n项和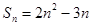 ,则
,则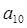 = 。
= 。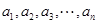 的前k项和为
的前k项和为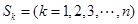 ,定义
,定义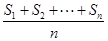 为该项数列的“凯森和”,如果项系数为99项的数列
为该项数列的“凯森和”,如果项系数为99项的数列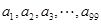 的“凯森和”为1000,那么项数为100的数列100,
的“凯森和”为1000,那么项数为100的数列100,