题目内容
已知数列{an}是首项a1=4,公比q≠1的等比数列,Sn是其前n项和,且4a1,a5,-2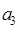 成等差数列.
成等差数列.
(1)求公比q的值;
(2)求Tn=a2+a4+a6+…+a2n的值.
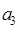 成等差数列.
成等差数列.(1)求公比q的值;
(2)求Tn=a2+a4+a6+…+a2n的值.
(1)q=-1.(2) Tn=na2=-4n.
本试题主要是考查了等比数列的通项公式的求解,以及等比数列的求和的综合运用。
(1)由题意得2a5=4a1-2a3.
∵{an}是等比数列且a1=4,公比q≠1,
∴2a1q4=4a1-2a1q2,∴q4+q2-2=0解得q的值。
(2)因为a2,a4,a6,…,a2n是首项为a2=4×(-1)=-4,公比为q2=1的等比数列,那么利用等比数列的前n项和公式得到结论。
解 (1)由题意得2a5=4a1-2a3.
∵{an}是等比数列且a1=4,公比q≠1,
∴2a1q4=4a1-2a1q2,∴q4+q2-2=0,
解得q2=-2(舍去)或q2=1,∴q=-1.
(2)∵a2,a4,a6,…,a2n是首项为a2=4×(-1)=-4,公比为q2=1的等比数列,∴Tn=na2=-4n.
(1)由题意得2a5=4a1-2a3.
∵{an}是等比数列且a1=4,公比q≠1,
∴2a1q4=4a1-2a1q2,∴q4+q2-2=0解得q的值。
(2)因为a2,a4,a6,…,a2n是首项为a2=4×(-1)=-4,公比为q2=1的等比数列,那么利用等比数列的前n项和公式得到结论。
解 (1)由题意得2a5=4a1-2a3.
∵{an}是等比数列且a1=4,公比q≠1,
∴2a1q4=4a1-2a1q2,∴q4+q2-2=0,
解得q2=-2(舍去)或q2=1,∴q=-1.
(2)∵a2,a4,a6,…,a2n是首项为a2=4×(-1)=-4,公比为q2=1的等比数列,∴Tn=na2=-4n.

练习册系列答案
相关题目
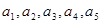 的各项均不等于0和1,此数列前
的各项均不等于0和1,此数列前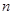 项的和为
项的和为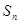 ,且满足
,且满足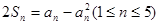 ,则满足条件的数列共有( )
,则满足条件的数列共有( )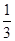 是较小的两份之和,则最小1份的大小是
是较小的两份之和,则最小1份的大小是 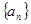 中,
中,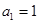 ,且对于任意正整数n,都有
,且对于任意正整数n,都有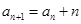 ,则
,则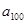 =______
=______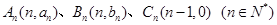 ,满足向量
,满足向量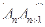 与向量
与向量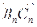 共线,且点
共线,且点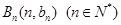 都在斜率为6的同一条直线上。若
都在斜率为6的同一条直线上。若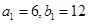 。求(1)数列
。求(1)数列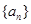 的通项
的通项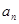 (2)数列{
(2)数列{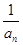 }的前n项和
}的前n项和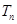
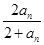 (n∈N*).
(n∈N*).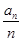 ,求数列{bn}的前n项和sn。
,求数列{bn}的前n项和sn。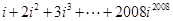 .
.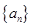 中,其前n项和为
中,其前n项和为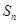 ,若对任意的正整数
,若对任意的正整数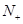 ,均有
,均有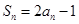 ,则
,则 ;
; 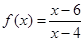
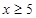 时
时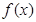 的取值范围;
的取值范围;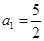 且
且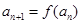 对任意
对任意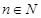 成立;
成立;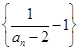 是等比数列;
是等比数列;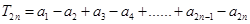 ,求证
,求证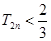 .
.