题目内容
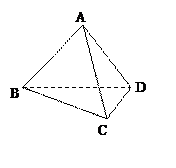
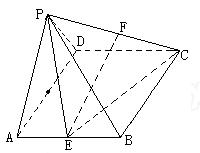
.(本小题12 分)如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD为正方形,E、F分别为AB、PC的中点.
①求证:EF⊥平面PCD;
②求平面PCB与平面PCD的夹角的余弦值.
①求证:EF⊥平面PCD;
②求平面PCB与平面PCD的夹角的余弦值.

(1)略
(2)
解:①证明:取AD中点为O,连接PO,∵平面PAD⊥平面ABCD,
∴PO⊥平面ABCD
故以OA为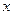 轴
轴
OP为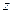 轴建立空间直角坐标系
轴建立空间直角坐标系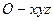 (如图所示)……1分
(如图所示)……1分
设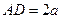 ,
,
则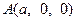 ,
,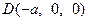 ,
,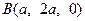 ,
,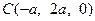 ,
,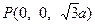
故可求得: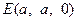 ,
,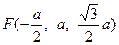 ……3分
……3分
∴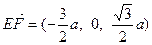 ,
,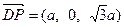 ,
,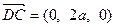
∵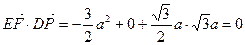 ,
,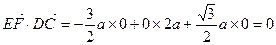
∴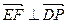 ,
,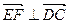 ∴
∴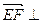 平面
平面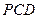
∴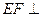 平面
平面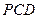 ……6分
……6分
②设平面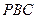 的一个法向量为
的一个法向量为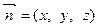 ,则
,则
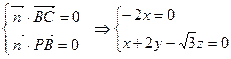 ,取
,取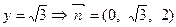 ……8分
……8分
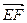 为平面
为平面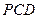 的一个法向量, ……9分
的一个法向量, ……9分
故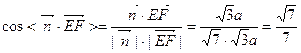 ……11分
……11分
故平面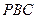 与平面
与平面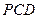 的夹角余弦值为
的夹角余弦值为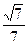 ……12分
……12分
∴PO⊥平面ABCD
故以OA为
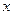 轴
轴OP为
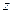 轴建立空间直角坐标系
轴建立空间直角坐标系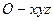 (如图所示)……1分
(如图所示)……1分设
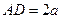 ,
,则
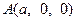 ,
,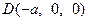 ,
,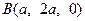 ,
,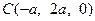 ,
,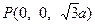
故可求得:
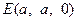 ,
,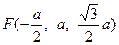 ……3分
……3分∴
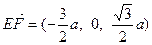 ,
,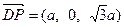 ,
,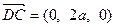
∵
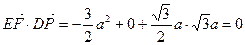 ,
,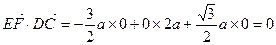
∴
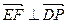 ,
,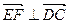 ∴
∴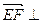 平面
平面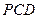
∴
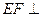 平面
平面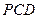 ……6分
……6分②设平面
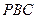 的一个法向量为
的一个法向量为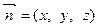 ,则
,则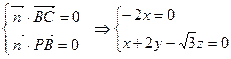 ,取
,取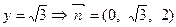 ……8分
……8分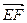 为平面
为平面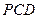 的一个法向量, ……9分
的一个法向量, ……9分故
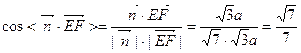 ……11分
……11分故平面
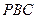 与平面
与平面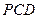 的夹角余弦值为
的夹角余弦值为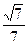 ……12分
……12分
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
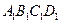 ,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.
,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.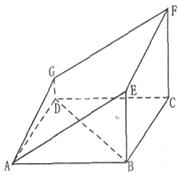

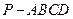 的底面
的底面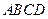 为一直角梯形,其中
为一直角梯形,其中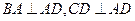 ,
,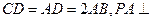 底面
底面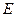 是
是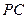 的中点.
的中点.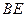 //平面
//平面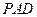 ;
;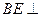 平面
平面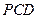 ,
,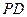 与
与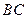 所成角的余弦值;
所成角的余弦值;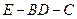 的余弦值.
的余弦值.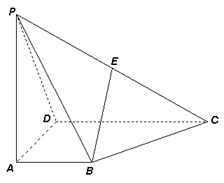
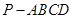 中,底面
中,底面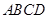 是直角梯形,
是直角梯形,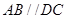 ,
,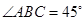 ,
,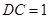 ,
,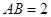 ,
,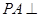 平面
平面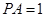 .
. 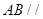 平面
平面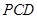 ;
;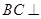 平面
平面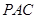 ;
;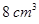 的正方体的顶点都在球面上,则球的体积是( )
的正方体的顶点都在球面上,则球的体积是( )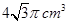
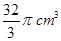
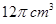
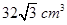
 )如图,棱锥
)如图,棱锥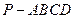 的底面
的底面 是矩形,
是矩形,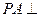 面
面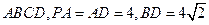 ,
,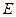 为
为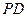 的中点.
的中点.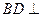 面
面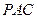 ;
; 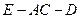 的余弦值;
的余弦值;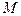 为
为 的中点,在棱
的中点,在棱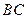 上是否存在点
上是否存在点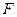 ,
,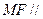 面
面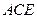 ?如果存在,请指出
?如果存在,请指出 点的位置;
点的位置;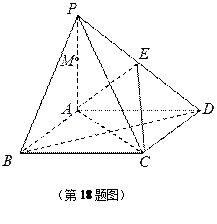
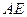 ;
; 如图,正方形
如图,正方形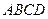 所在平面与
所在平面与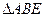 所在平面垂直,
所在平面垂直,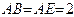 ,
,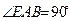 ,
,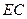 中点为
中点为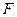 .
.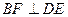
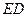 与平面
与平面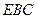 所成角
所成角
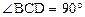 ,
,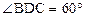 ,
,