题目内容
12．函数f（x）=-2sin2x+2cos x的最小值和最大值分别是（ ）| A． | -2，2 | B． | -2，$\frac{5}{2}$ | C． | -$\frac{1}{2}$，2 | D． | -$\frac{5}{2}$，2 |
分析 由条件利用同角三角函数的基本关系化简函数的解析式，再利用二次函数的性质求得函数f（x）取得最小值和最大值．
解答 解：函数f（x）=-2sin2x+2cosx=2cos2x+2cosx-2=2${（cosx+\frac{1}{2}）}^{2}$-$\frac{5}{2}$，
再根据cosx∈[-1，1]，可得当cosx=-$\frac{1}{2}$时，函数f（x）取得最小值为-$\frac{5}{2}$，
当cosx=1时，函数f（x）取得最大值为2，
故选：D．
点评 本题主要考查同角三角函数的基本关系、二次函数的性质应用，属于基础题．
练习册系列答案
相关题目
3．已知点A（a，-5），B（0，10）间的距离是17，则a的值是（ ）
| A． | 8 | B． | -8 | C． | ±4 | D． | ±8 |
1．
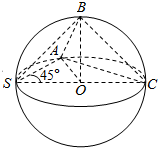已知球的直径SC=4，A，B是该球球面上的两点，AB=2，∠ASC=∠BSC=45°，则棱锥S-ABC的体积为（ ）
已知球的直径SC=4，A，B是该球球面上的两点，AB=2，∠ASC=∠BSC=45°，则棱锥S-ABC的体积为（ ）| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{5\sqrt{3}}{3}$ | D． | $\frac{4\sqrt{3}}{3}$ |