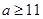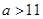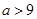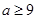题目内容
已知x∈(0,+∞)时,不等式9x-m·3x+m+1>0恒成立,则m的取值范围是( )
A.2-2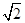 <m<2+2 <m<2+2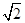 | B.m<2 |
C.m<2+2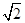 | D.m≥2+2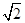 |
C
令t=3x(t>1),则由已知得函数f(t)=t2-mt+m+1(t∈(1,+∞))的图象恒在x轴的上方,
即Δ=(-m)2-4(m+1)<0或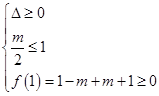
解得m<2+2 .
.
即Δ=(-m)2-4(m+1)<0或
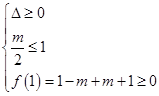
解得m<2+2
 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
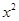 -(
-(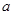 +
+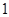 )
)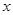 +
+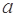 ∈R).
∈R). 的解集与关于
的解集与关于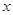 的不等式
的不等式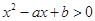 的解集相同.
的解集相同.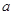 ,
,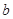 的值;
的值;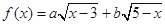 的最大值,以及取得最大值时
的最大值,以及取得最大值时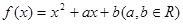 ,方程
,方程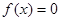 有两个相等的实数根,若关于
有两个相等的实数根,若关于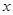 的不等式
的不等式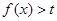 的解集为
的解集为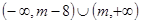 ,则实数
,则实数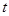 的值为 .
的值为 .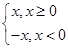 ,则不等式x+xf(x)≤2的解集是________.
,则不等式x+xf(x)≤2的解集是________.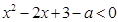 成立的一个充分条件是
成立的一个充分条件是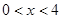 ,则实数
,则实数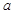 的取值范围应为
的取值范围应为