题目内容
【题目】已知椭圆的中心在原点,一个长轴端点为![]() ,离心率
,离心率![]() ,过P分别作斜率为
,过P分别作斜率为![]() 的直线PA,PB,交椭圆于点A,B。
的直线PA,PB,交椭圆于点A,B。
(1)求椭圆的方程;
(2)若![]() ,则直线AB是否经过某一定点?
,则直线AB是否经过某一定点?
【答案】(1)![]() (2)直线AB恒过点
(2)直线AB恒过点![]()
【解析】
试题分析:(1)设椭圆的方程为![]() (a>b>0),根据题意建立关于a、b的方程组解出a、b之值,即可得到椭圆的方程;(2)由题意得直线PA方程为y=k1x-2,与椭圆方程消去y得到关于x的方程,解出A点坐标含有k1的式子,同理得到B点坐标含有k2的式子,利用直线的两点式方程列式并结合k1k2=2化简整理,可证出AB方程当x=0时y=-6,由此可得直线AB必过定点Q(0,-6).
(a>b>0),根据题意建立关于a、b的方程组解出a、b之值,即可得到椭圆的方程;(2)由题意得直线PA方程为y=k1x-2,与椭圆方程消去y得到关于x的方程,解出A点坐标含有k1的式子,同理得到B点坐标含有k2的式子,利用直线的两点式方程列式并结合k1k2=2化简整理,可证出AB方程当x=0时y=-6,由此可得直线AB必过定点Q(0,-6).
试题解析:(1)易得椭圆的方程![]()
(2)直线PA,PB的方程分别为![]() 由
由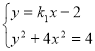 得
得![]() ,解得
,解得![]() 或
或![]() ,于是
,于是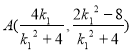 ,同理
,同理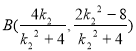 。
。
直线PA,PB的方程分别为![]() 由
由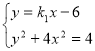 得
得![]() ,解得
,解得![]() 或
或![]() ,于是
,于是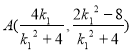 ,同理
,同理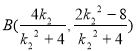 。由
。由![]() 得
得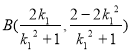 ,
,![]() 直线
直线![]() :
: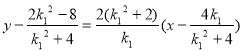 ,
,
令![]() 得
得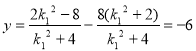 ,则直线AB恒过点
,则直线AB恒过点![]()

练习册系列答案
相关题目