题目内容
已知函数 .
.
(I)若 在
在 处取得极值,
处取得极值,
①求 、
、 的值;②存在
的值;②存在 ,使得不等式
,使得不等式 成立,求
成立,求 的最小值;
的最小值;
(II)当 时,若
时,若 在
在 上是单调函数,求
上是单调函数,求 的取值范围.(参考数据
的取值范围.(参考数据 )
)
(1)①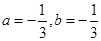 ,②
,② ;(2)
;(2)
解析试题分析:(1)①根据 在
在 处取得极值,求导将
处取得极值,求导将 带入到导函数中,联立方程组求出
带入到导函数中,联立方程组求出 的值;②存在性恒成立问题,
的值;②存在性恒成立问题, ,只需
,只需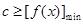 ,进入通过求导求出
,进入通过求导求出 的极值,最值.(2)当
的极值,最值.(2)当 的未知时,要根据
的未知时,要根据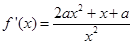 中分子是二次函数形式按
中分子是二次函数形式按 进行讨论.
进行讨论.
试题解析:(1) 定义域为
定义域为 .
.
①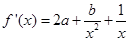 ,
,
因为 在
在 处取和极值,故
处取和极值,故 ,
,
即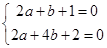 ,解得
,解得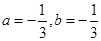 .
.
②由题意:存在 ,使得不等式
,使得不等式 成立,则只需
成立,则只需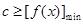
由 ,令
,令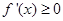 则
则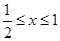 ,令
,令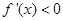 则
则 或
或 ,
,
所以 在
在 上单调递减,
上单调递减, 在
在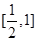 上单调递增,
上单调递增, 在
在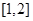 上单调递减
上单调递减
所以 在
在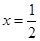 处取得极小值,
处取得极小值,
而最大值需要比较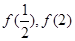 的大小,
的大小, ,
,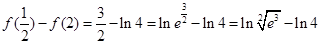 ,
,
比较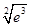 与4的大小,而
与4的大小,而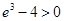 ,所以
,所以

所以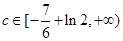
所以 .
.
(2)当  时,
时,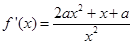
①当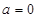 时,
时, 则
则 在
在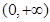 上单调递增;
上单调递增;
②当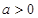 时,∵
时,∵ 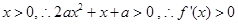 ,则
,则 在
在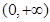 上单调递增;
上单调递增;
③当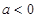 时,设
时,设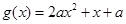 ,只需
,只需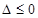 ,从而得
,从而得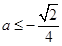 ,此时
,此时 在
在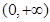 上单调递减;
上单调递减;
综上可得, .
.
考点:1.利用导数求函数的极值、最值;2.函数恒成立问题;3.利用单调性求参数范围.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
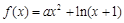 .
.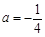 时,求函数
时,求函数 的单调区间;
的单调区间;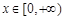 时,不等式
时,不等式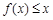 恒成立,求实数
恒成立,求实数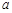 的取值范围.
的取值范围.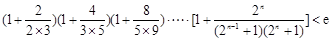 (
(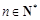 ,e是自然对数的底数).
,e是自然对数的底数). 在
在 处取得极值。
处取得极值。 ;
; ,使得对任意
,使得对任意 ?若存在,求
?若存在,求 (
( 为常数)
为常数)  的单调区间;
的单调区间; 时,
时, ,求
,求 ,
, ,
, (1)若
(1)若 ,求函数
,求函数 的极值;
的极值; 在
在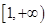 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围; 的图象上是否存在不同的两点
的图象上是否存在不同的两点 ,使线段
,使线段 的中点的横坐标
的中点的横坐标 与直线
与直线 之间满足
之间满足 ?若存在,求出
?若存在,求出 ,其中
,其中 是常数且
是常数且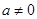 .
. 时,
时, 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围;
的取值范围; 时,讨论
时,讨论 是正整数,证明:
是正整数,证明: .
. .
. 在
在 处的切线方程为
处的切线方程为 ,求实数
,求实数 的值.
的值. 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数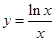 在点(1,0)处的切线.
在点(1,0)处的切线.