题目内容
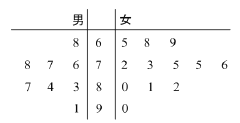
【题目】在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0. 若B的坐标为(1,2),求△ABC三边所在直线方程及点C坐标.
【答案】BC: 2x+y-4=0. AB:x-y+1=0, AC:x+y+1=0,C(5,-6)
【解析】试题分析:由![]() 边上的高所在的直线方程为x-2y+1=0,可得直线
边上的高所在的直线方程为x-2y+1=0,可得直线![]() 的斜率,又B的坐标为(1,2),由点斜式可得直线
的斜率,又B的坐标为(1,2),由点斜式可得直线![]() 的方程;由
的方程;由![]() 边上的高所在的直线方程与角
边上的高所在的直线方程与角![]() 的平分线方程联立可得点
的平分线方程联立可得点![]() 的坐标,利用两点式可得直线
的坐标,利用两点式可得直线![]() 的方程,根据直线的对称性列可求出直线
的方程,根据直线的对称性列可求出直线![]() 的方程;直线
的方程;直线![]() 的方程与直线
的方程与直线![]() 的方程联立可得
的方程联立可得![]() 点的坐标.
点的坐标.
试题解析:BC边上高AD所在直线方程x-2y+1=0,
∴kBC=-2,
∴BC边所在直线方程为:y-2=-2(x-1)即2x+y-4=0.
由![]() ,得A(-1,0),
,得A(-1,0),
∴直线AB:x-y+1=0,点B(1,2)关于y=0的对称点B′(1,-2)在边AC上,
∴直线AC:x+y+1=0,
由![]() ,得点C(5,-6).
,得点C(5,-6).

 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】(本小题满分12分)
甲乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下的列联表:
班级与成绩列联表
优 秀 | 不优秀 | |
甲 班 | 10 | 35 |
乙 班 | 7 | 38 |
根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为成绩与班级有关系?
附:
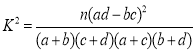
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】某种商品在![]() 天每件的销售价格
天每件的销售价格![]() (元)与时间
(元)与时间![]() (天)的函数关系用如图表示,该商品在
(天)的函数关系用如图表示,该商品在![]() 天内日销售量
天内日销售量![]() (件)与时间
(件)与时间![]() (天)之间的关系如下表:
(天)之间的关系如下表:
|
|
|
|
|
|
|
|
|
|

(![]() )根据提供的图象(如图),写出该商品每件的销售价格
)根据提供的图象(如图),写出该商品每件的销售价格![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
(![]() )根据表
)根据表![]() 提供的数据,写出日销售量
提供的数据,写出日销售量![]() 与时间
与时间![]() 的一次函数关系式.
的一次函数关系式.
(![]() )求该商品的日销售金额的最大值,并指出日销售金额最大的一天是
)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是![]() 天中的第几天.(日销售金额
天中的第几天.(日销售金额![]() 每件的销售价格
每件的销售价格![]() 日销售量)
日销售量)