题目内容
【题目】如图，在直三棱柱
中，
，
，
，
.
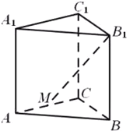
（1）求三棱柱的体积；
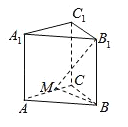
（2）若点M是棱AC的中点，求直线
与平面ABC所成的角的大小.
【答案】（1）
（2）
【解析】
（1）由直三棱柱ABC﹣A1B1C1中，∠ABC＝60°，BB1＝3，AB＝4，BC＝4．能求出三棱柱ABC﹣A1B1C1的体积．
（2）点M是棱AC的中点，B1M在平面ABC的射影为直线MB，则∠B1MB就是直线B1M与平面ABC所成的角的大小，由此能求出直线B1M与平面ABC所成的角的大小．
（1）∵在直三棱柱ABC﹣A1B1C1中，
∠ABC＝60°，BB1＝3，AB＝4，BC＝4．
∴三棱柱ABC﹣A1B1C1的体积：
V
12
．
（2）点M是棱AC的中点，
B1M在平面ABC的射影为直线MB，
则∠B1MB就是直线B1M与平面ABC所成的角的大小，
tan∠B1MB
，
∴∠B1MB＝arctan
．
∴直线B1M与平面ABC所成的角的大小为arctan．
阅读快车系列答案
【题目】某网络平台从购买该平台某课程的客户中，随机抽取了100位客户的数据，并将这100个数据按学时数，客户性别等进行统计，整理得到如表：
学时数 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
（1）根据上表估计男性客户购买该课程学时数的平均值（同一组中的数据用该组区间的中点值作代表，结果保留小数点后两位）；
（2）从这100位客户中，对购买该课程学时数在20以下的女性客户按照分层抽样的方式随机抽取7人，再从这7人中随机抽取2人，求这2人购买的学时数都不低于15的概率．
（3）将购买该课程达到25学时及以上者视为“十分爱好该课程者”，25学时以下者视，为“非十分爱好该课程者”．请根据已知条件完成以下
列联表，并判断是否有99．9%的把握认为“十分爱好该课程者”与性别有关？
非十分爱好该课程者 | 十分爱好该课程者 | 合计 | |
男性 | |||
女性 | |||
合计 | 100 |
附：
，
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
