题目内容
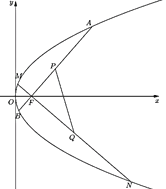
【题目】已知F1，F2分别是椭圆C：
1（＞b＞0）的左、右焦点，过F2且不与x轴垂直的动直线l与椭圆交于M，N两点，点P是椭圆C右准线上一点，连结PM，PN，当点P为右准线与x轴交点时有2PF2＝F1F2．
（1）求椭圆C的离心率；
（2）当点P的坐标为（2，1）时，求直线PM与直线PN的斜率之和．
【答案】(1) e
；(2)2
【解析】
（1）由
，建立
，
的关系，求出离心率即可；
（2）先求出椭圆的方程，设直线的方程并于椭圆联立，代入
与直线
的斜率之和的表达式中，求出即可．
解：（1）当
为右准线与
轴交点时有，
，
，
，又
，
所以
；
（2）
，
，又
，
，
，
，所以
，
所以椭圆的方程为：
，
设直线
，
，
，
，
，
联立
，消去
，得
，
则
，
，
，
所以直线与直线的斜率之和为2．
练习册系列答案
名校课堂系列答案
相关题目
