Question

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，且∠DAB＝60°．点E是棱PC的中点，平面ABE与棱PD交于点F．

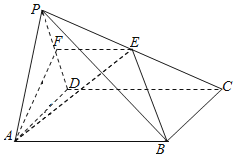
（1）求证：AB∥EF；

（2）若PA＝PD＝AD，且平面PAD⊥平面ABCD，求平面PAF与平面AFE所成的锐二面角的余弦值．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）先证明平面即可；（2）建立空间直角坐标系，分别求出平面、平面的法向量，再由向量的夹角公式计算即可．

证明：（1）因为底面ABCD是菱形，所以AB∥CD．

又因为AB面PCD，CD面PCD，所以AB∥面PCD．

又因为A，B，E，F四点共面，且平面ABEF∩平面PCD＝EF，

所以AB∥EF．

解：（2）取AD中点G，连接PG，GB．

因为PA＝PD，所以PG⊥AD．

又因为平面PAD⊥平面ABCD，

且平面PAD∩平面ABCD＝AD，

所以PG⊥平面ABCD．所以PG⊥GB．

在菱形ABCD中，因为AB＝AD，∠DAB＝60°，G是AD中点，

所以AD⊥GB．

如图，以G为原点，GA为x轴，GB为y轴，GP为z轴，建立空间直角坐标系G﹣xyz．

设PA＝PD＝AD＝2a，

则G（0，0，0），A（a，0，0），．

又因为AB∥EF，点E是棱PC中点，所以点F是棱PD中点．

所以，．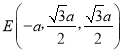

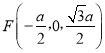所以，．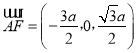

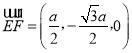设平面AFE的法向量为n＝（x，y，z），则有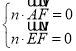所以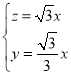

令x＝3，则平面AFE的一个法向量为．

因为BG⊥平面PAD，所以是平面PAF的一个法向量．

因为，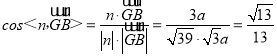

所以平面PAF与平面AFE所成的锐二面角的余弦值为．