题目内容
已知中心在原点,长轴在x轴上的椭圆的两准线间的距离为2 ,若椭圆被直线x+y+1=0截得的弦的中点的横坐标是
,若椭圆被直线x+y+1=0截得的弦的中点的横坐标是 ,求椭圆的方程
,求椭圆的方程
 ,若椭圆被直线x+y+1=0截得的弦的中点的横坐标是
,若椭圆被直线x+y+1=0截得的弦的中点的横坐标是 ,求椭圆的方程
,求椭圆的方程解法一:
令椭圆方程为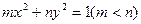 ,
,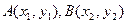 由题得:
由题得: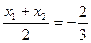 ,
,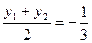
由 可得
可得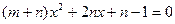 ,
,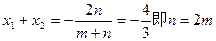
又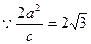 即
即
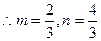
椭圆方程为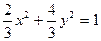
解法二:
令椭圆方程为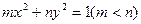 ,
,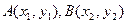 由题得:
由题得: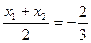 ,
,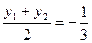
由 作差得
作差得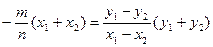
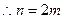
又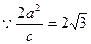 即
即
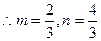
椭圆方程为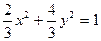
令椭圆方程为
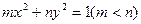 ,
,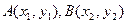 由题得:
由题得: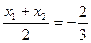 ,
,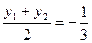
由
 可得
可得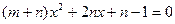 ,
,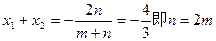
又
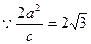 即
即
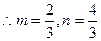
椭圆方程为
解法二:
令椭圆方程为
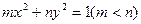 ,
,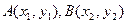 由题得:
由题得: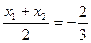 ,
,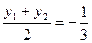
由
 作差得
作差得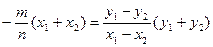
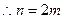
又
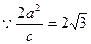 即
即
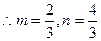
椭圆方程为
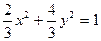
椭圆中心定,焦点定,所以椭圆的位置定,而且由准线方程可得一个方程,还有一个方程怎么找?根据直线与椭圆相交,可联立方程组,利用韦达定理解决,事实上就是把交点问题化归为方程根的问题,有关中点问题还可设弦的两端点坐标代入椭圆方程相减,式中含有 三个未知量,但直接联系了中点和直线的斜率,同样可得到a与b的关系(点差法)从而解决问题,但两者又各有弊端:韦达定理解决过程中易漏解,需关注直线的斜率问题;点差法则在确定范围方面略显不足。
三个未知量,但直接联系了中点和直线的斜率,同样可得到a与b的关系(点差法)从而解决问题,但两者又各有弊端:韦达定理解决过程中易漏解,需关注直线的斜率问题;点差法则在确定范围方面略显不足。
 三个未知量,但直接联系了中点和直线的斜率,同样可得到a与b的关系(点差法)从而解决问题,但两者又各有弊端:韦达定理解决过程中易漏解,需关注直线的斜率问题;点差法则在确定范围方面略显不足。
三个未知量,但直接联系了中点和直线的斜率,同样可得到a与b的关系(点差法)从而解决问题,但两者又各有弊端:韦达定理解决过程中易漏解,需关注直线的斜率问题;点差法则在确定范围方面略显不足。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
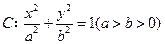 的左、右焦点分别是
的左、右焦点分别是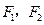 ,离心率为
,离心率为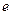 .直线
.直线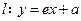 与
与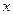 轴,
轴,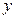 轴分别交于点
轴分别交于点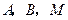 是直线
是直线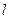 与椭圆
与椭圆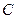 的一个公共点,
的一个公共点,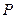 是点
是点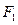 关于直线
关于直线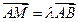 .
.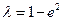 ;
;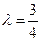 ,
,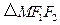 的周长为
的周长为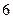 ,写出椭圆
,写出椭圆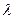 的值,使得
的值,使得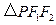 是等腰三角形.
是等腰三角形. (
( ),过椭圆中心O作互相垂直的两条弦AC、BD,设点A、B的离心角分别为
),过椭圆中心O作互相垂直的两条弦AC、BD,设点A、B的离心角分别为 和
和 ,求
,求 的取值范围。
的取值范围。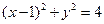 与
与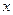 轴负半轴交于B点,过B的弦BE与
轴负半轴交于B点,过B的弦BE与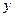 轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆。(1)求椭圆的方程;(2)点P在椭圆C上运动,点Q在圆A上运动,求PQ+PD的最大值。
轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆。(1)求椭圆的方程;(2)点P在椭圆C上运动,点Q在圆A上运动,求PQ+PD的最大值。
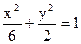 的焦点,P是曲线C2∶
的焦点,P是曲线C2∶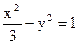 与C1的一个交点,求的值.
与C1的一个交点,求的值. 是两个定点,以
是两个定点,以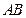 为一条底边作梯形
为一条底边作梯形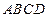 ,使
,使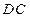 的长为定值,
的长为定值,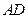 与
与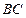 的长之和也是定值,则
的长之和也是定值,则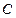 点的轨迹是什么曲线?
点的轨迹是什么曲线? 的内接矩形的面积的最大值为
的内接矩形的面积的最大值为  是三角形的一个内角,且
是三角形的一个内角,且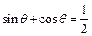 ,则方程
,则方程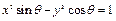 表示
表示