题目内容
20.设非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是$\frac{5π}{6}$,且|$\overrightarrow{a}$|=|$\overrightarrow{a}+\overrightarrow{b}$|,则$\frac{|\overrightarrow{a}+t\overrightarrow{b}|}{|\overrightarrow{b}|}$(t∈R)的最小值是$\frac{\sqrt{3}}{6}$.分析 由已知利用模的等式两边平方得到|$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|,将所求平方利用此关系得到关于t的二次函数解析式,然后求最小值
解答 解:因为非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是$\frac{5π}{6}$,且|$\overrightarrow{a}$|=|$\overrightarrow{a}+\overrightarrow{b}$|,
所以|$\overrightarrow{a}$|2=|$\overrightarrow{a}+\overrightarrow{b}$|2,所以|$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$|,
则($\frac{|\overrightarrow{a}+t\overrightarrow{b}|}{|\overrightarrow{b}|}$)2=$\frac{{\overrightarrow{a}}^{2}+{t}^{2}{\overrightarrow{b}}^{2}+2t\overrightarrow{a}•\overrightarrow{b}}{{\overrightarrow{b}}^{2}}$=t2-t+$\frac{1}{3}$=(t-$\frac{1}{2}$)2+$\frac{1}{12}$,
所以当t=$\frac{1}{2}$时,则$\frac{|\overrightarrow{a}+t\overrightarrow{b}|}{|\overrightarrow{b}|}$的最小值为$\sqrt{\frac{1}{12}}=\frac{\sqrt{3}}{6}$;
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题考查了向量的数量积公式的运用以及向量的平方与模的平方相等的运用,关键是将所求转化为关于t 的二次函数求最值.属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -$\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
| A. | (1,2) | B. | [1,2] | C. | [1,2) | D. | (1,2] |
| A. | -$\frac{8}{3}$ | B. | -6 | C. | 6 | D. | $\frac{8}{3}$ |
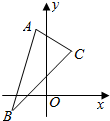 已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).
已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).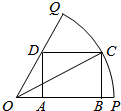 如图,已知OPQ是半径为$\sqrt{7}$圆心角为$\frac{π}{3}$的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
如图,已知OPQ是半径为$\sqrt{7}$圆心角为$\frac{π}{3}$的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.