题目内容
函数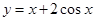 在区间
在区间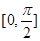 上的最大值是 .
上的最大值是 .
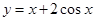 在区间
在区间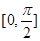 上的最大值是 .
上的最大值是 .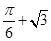
试题分析:对函数y=x+2cosx进行求导,研究函数在区间[
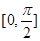 上的极值,本题极大值就是最大值.解:∵y=x+2cosx,∴y′=1-2sinx,令y′=0而x∈[0,
上的极值,本题极大值就是最大值.解:∵y=x+2cosx,∴y′=1-2sinx,令y′=0而x∈[0,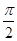 ]则x=
]则x=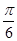 当x∈[0,
当x∈[0,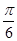 ]时,y′>0.当x∈[
]时,y′>0.当x∈[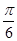 ,
,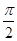 ]时,y′<0.所以当x=
]时,y′<0.所以当x=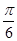 时取极大值,也是最大值;故答案为
时取极大值,也是最大值;故答案为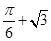
点评:本题考查了利用导数求闭区间上函数的最大值问题,属于导数的基础题.

练习册系列答案
相关题目
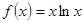 ,
,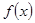 的极值点;
的极值点;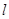 过点
过点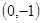 ,并且与曲线
,并且与曲线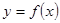 相切,求直线
相切,求直线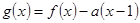 ,其中
,其中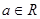 ,求函数
,求函数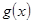 在
在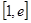 上的最小值(其中
上的最小值(其中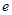 为自然对数的底数).
为自然对数的底数).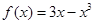 ,当
,当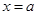 时取得极小值
时取得极小值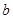 ,则
,则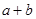 等于( )
等于( )



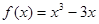
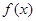 的单调区间;
的单调区间;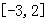 上的最值.
上的最值.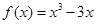
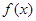 的单调区间;
的单调区间;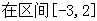 上的最值.
上的最值.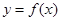 在(
在(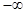 ,+
,+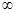 )内有意义.对于给定的正数K,已知函数
)内有意义.对于给定的正数K,已知函数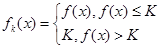 ,取函数
,取函数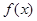 =
=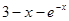 .若对任意的
.若对任意的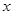
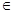 (
(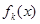 =
= ,且
,且 在
在 和
和 处取得极值.
处取得极值. ,是否存在实数
,是否存在实数 ,使得曲线
,使得曲线 与
与 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出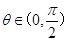 ,则函数
,则函数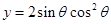 的值域为 __________ .
的值域为 __________ .