Question

【题目】如图，在菱形 中， ⊥平面 ，且四边形 是平行四边形．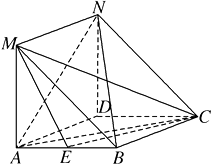

（1）求证： ；
（2）当点 在 的什么位置时，使得 ∥平面 ，并加以证明．

Answer 1

【答案】
（1）证明：连接BD ， 则AC⊥BD.
由已知得DN⊥平面ABCD ， 因为AC平面ABCD ， 所以DN⊥AC.
因为DN平面NDB ， BD平面NDB ， DN∩DB＝D ，
所以AC⊥平面NDB.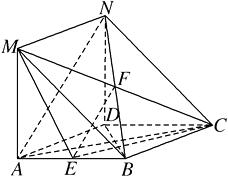

又BN平面NDB ，
所以AC⊥BN.
（2）解：当E为AB的中点时，有AN∥平面MEC.
设CM与BN交于F ， 连接EF.
由已知可得四边形BCNM是平行四边形，F是BN的中点，
因为E是AB的中点，
所以AN∥EF.
又EF平面MEC ， AN平面MEC ，
所以AN∥平面MEC.
【解析】（1）要证明AC⊥BN，只要证明AC⊥平面NDB，而由已知可知AC⊥BD，则只要证出AC⊥DN，结合已知容易证明
（2）当E为AB的中点时，设CM与BN交于F，由已知可得AN∥EF，结合线面平行的判定定理可证.