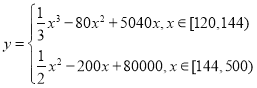题目内容
【题目】已知函数f(x)= ![]() .
.
(1)证明:f(x)+|f(x)﹣2|≥2;
(2)当x≠﹣1时,求y= ![]() 的最小值.
的最小值.
【答案】
(1)证明:因为f(x)= ![]() ≥0,
≥0,
所以f(x)+|f(x)﹣2|=|f(x)|+|2﹣f(x)|≥|f(x)+2﹣f(x)|=2,
当且仅当f(x)[2﹣f(x)]≥0即0≤f(x)≤2即﹣1﹣2 ![]() ≤x≤﹣1+2
≤x≤﹣1+2 ![]() 时取等号
时取等号
(2)解:当x≠﹣1时,f(x)= ![]() >0,
>0,
所以y= ![]() =
= ![]() +
+ ![]() +[f(x)]2≥3
+[f(x)]2≥3 ![]() =
= ![]() ,
,
当且仅当 ![]() =
= ![]() =[f(x)]2即x=﹣1±
=[f(x)]2即x=﹣1± ![]() 时取等号,
时取等号,
所以所求最小值为 ![]()
【解析】(1)通过绝对值不等式放缩可得结论;(2)通过当x≠﹣1时f(x)= ![]() >0,利用基本不等式的推广放缩可得结论.
>0,利用基本不等式的推广放缩可得结论.
【考点精析】根据题目的已知条件,利用函数的最值及其几何意义的相关知识可以得到问题的答案,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目