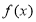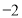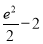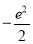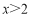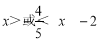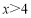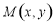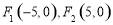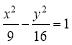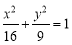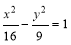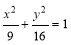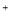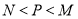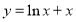题目内容
设一个焦点为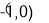 ,且离心率
,且离心率 的椭圆
的椭圆 上下两顶点分别为
上下两顶点分别为 ,直线
,直线 交椭圆
交椭圆 于
于 两点,直线
两点,直线 与直线
与直线 交于点
交于点 .
.
(1)求椭圆 的方程;
的方程;
(2)求证: 三点共线.
三点共线.
(1)  (2) 详见解析.
(2) 详见解析.
【解析】
试题分析:(1)利用椭圆的定义和几何性质;(2)直线与圆锥曲线相交问题,可以设而不求,联立直线与椭圆方程,利用韦达定理结合题目条件来证明.
试题解析:(1)由题知 ,
,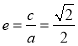 ,∴
,∴ , 3分
, 3分
∴椭圆 .4分
.4分
(2) 设点 ,由(1)知
,由(1)知
∴直线 的方程为
的方程为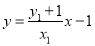 ,∴
,∴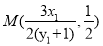 .5分
.5分
∴ ,
,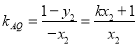 ,8分
,8分
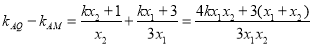
由方程组
化简得: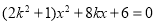 ,
,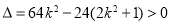 ,
,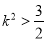 .
.
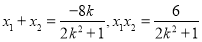 10分
10分
∴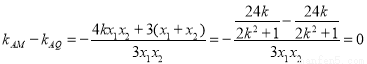 ,
,
∴ 三点共线.12分
三点共线.12分
考点:1.椭圆的标准方程;2.直线与圆锥曲线相交问题;3.韦达定理.

练习册系列答案
相关题目