题目内容
已知函数 的图象在
的图象在 上连续,定义:
上连续,定义: ,
,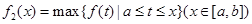 .其中,
.其中, 表示函数
表示函数 在
在 上的最小值,
上的最小值, 表示函数
表示函数 在
在 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数 ,使得
,使得 对任意的
对任意的 成立,则称函数
成立,则称函数 为
为 上的“
上的“ 阶收缩函数”.
阶收缩函数”.
(Ⅰ)若 ,试写出
,试写出 ,
, 的表达式;
的表达式;
(Ⅱ)已知函数 ,试判断
,试判断 是否为
是否为 上的“
上的“ 阶收缩函数”.如果是,求出对应的
阶收缩函数”.如果是,求出对应的 ;如果不是,请说明理由;
;如果不是,请说明理由;
(Ⅲ)已知 ,函数
,函数 是
是 上的2阶收缩函数,求
上的2阶收缩函数,求 的取值范围.
的取值范围.
(Ⅰ)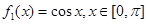 ,
,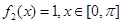 ;(Ⅱ)存在k=4,使得f(x)是[﹣1,4]上的4阶收缩函数.(Ⅲ)
;(Ⅱ)存在k=4,使得f(x)是[﹣1,4]上的4阶收缩函数.(Ⅲ)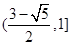
解析试题分析:(Ⅰ)根据f(x)=cosx的最大值为1,可得f1(x)、f2(x)的解析式.
(Ⅱ)根据函数f(x)=x2在x∈[-1,4]上的值域,先写出f1(x)、f2(x)的解析式,再由f2(x)-f1(x)≤k(x-a)求出k的范围得到答案.
(3)先对函数f(x)进行求导判断函数的单调性,进而写出f1(x)、f2(x)的解析式,
然后再由f2(x)-f1(x)≤k(x-a)求出k的范围得到答案.
试题解析:
(Ⅰ)由题意可得: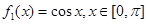 ,
,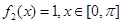 2分
2分
(Ⅱ)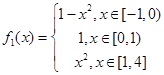 ,
,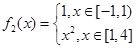 ,
,
所以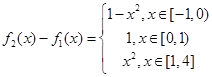 4分
4分
当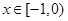 时,
时,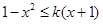 ,∴
,∴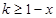 ,即
,即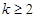 ;
;
当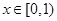 时,
时,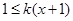 ,∴
,∴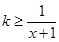 ,即
,即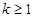 ;
;
当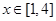 时,
时,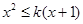 ,∴
,∴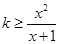 ,即
,即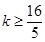 .
.
综上所述,∴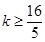
即存在k=4,使得f(x)是[﹣1,4]上的4阶收缩函数. 7分
(Ⅲ)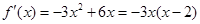 令
令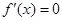 得
得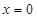 或
或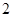 .函数f(x)的变化情况如下:
.函数f(x)的变化情况如下:x (- 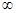 ,0)
,0)0 (0,2) 2 (2,+ 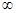 )
)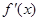
- 0 + 0 - f(x) 
0 
4 
核心360小学生赢在100系列答案
期末闯关100分系列答案
家校导学系列答案
新每课一练系列答案

黄冈海淀大考卷单元期末冲刺100分系列答案

课堂新动态系列答案

初中历史与社会思想品德精讲精练系列答案
 (其中
(其中 ,e是自然对数的底数).
,e是自然对数的底数). ,试判断函数
,试判断函数 在区间
在区间 上的单调性;
上的单调性; ,当
,当 时,试比较
时,试比较 ,
, (
( ),求k的取值范围,并证明
),求k的取值范围,并证明 .
. .
. 在
在 处取得极值,求实数
处取得极值,求实数 的值;
的值; 上的最大值.
上的最大值. (其中
(其中 为常数).
为常数).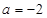 时,求函数
时,求函数 的最值;
的最值;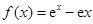 .
. 的最小值;
的最小值;
 ;
;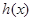 与
与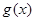 定义域上的任意实数
定义域上的任意实数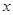 ,若存在常数
,若存在常数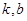 ,使得
,使得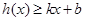 和
和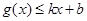 都成立,则称直线
都成立,则称直线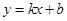 为函数
为函数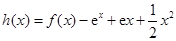 ,
,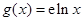 ,
, ,
, .
. ,求证:当
,求证:当 时,
时, ;
; 在区间
在区间 上单调递增,试求
上单调递增,试求 的取值范围;
的取值范围; .
. 的反函数为
的反函数为 ,设
,设 的图象上在点
的图象上在点 处的切线在y轴上的截距为
处的切线在y轴上的截距为 ,数列{
,数列{ }满足:
}满足:
 中,仅
中,仅 最小,求
最小,求 的取值范围;
的取值范围; 数列
数列 满足
满足 ,求证:对一切n≥2的正整数都有
,求证:对一切n≥2的正整数都有
 ,点
,点 为一定点,直线
为一定点,直线 分别与函数
分别与函数 的图象和
的图象和 轴交于点
轴交于点 ,
, ,记
,记 的面积为
的面积为 .
. 时,求函数
时,求函数 时, 若
时, 若 ,使得
,使得 , 求实数
, 求实数 的取值范围.
的取值范围.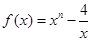 ,且
,且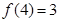 .
. 的奇偶性并说明理由;
的奇偶性并说明理由;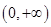 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;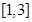 上,不等式
上,不等式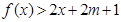 恒成立,试确定实数
恒成立,试确定实数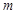 的取值范围.
的取值范围.