题目内容
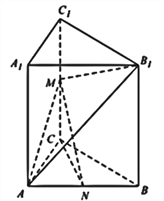
【题目】如图,已知正四面体D﹣ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB, ![]() =
= ![]() =2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则( )
=2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则( )
A.γ<α<β
B.α<γ<β
C.α<β<γ
D.β<γ<α
【答案】B
【解析】解法一:如图所示,建立空间直角坐标系.设底面△ABC的中心为O.
不妨设OP=3.则O(0,0,0),P(0,﹣3,0),C(0,﹣6,0),D(0,0,6 ![]() ),
),
Q ![]() ,R
,R ![]() ,
,![]() =
= ![]() ,
, ![]() =(0,3,6
=(0,3,6 ![]() ),
), ![]() =(
=( ![]() ,5,0),
,5,0), ![]() =
= ![]() ,
,![]() =
= ![]() .
.
设平面PDR的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 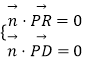 ,可得
,可得 ![]() ,
,
可得 ![]() =
= ![]() ,取平面ABC的法向量
,取平面ABC的法向量 ![]() =(0,0,1).
=(0,0,1).
则cos ![]() =
= ![]() =
= ![]() ,取α=arccos
,取α=arccos ![]() .
.
同理可得:β=arccos ![]() .γ=arccos
.γ=arccos ![]() .
.
∵ ![]() >
> ![]() >
> ![]() .
.
∴α<γ<β.
解法二:如图所示,连接OD,OQ,OR,过点O发布作垂线:OE⊥DR,OF⊥DQ,OG⊥QR,垂足分别为E,F,G,连接PE,PF,PG.
设OP=h.
则cosα= ![]() =
= ![]() =
= ![]() .
.
同理可得:cosβ= ![]() =
= ![]() ,cosγ=
,cosγ= ![]() =
= ![]() .
.
由已知可得:OE>OG>OF.
∴cosα>cosγ>cosβ,α,β,γ为锐角.
∴α<γ<β.
故选:B.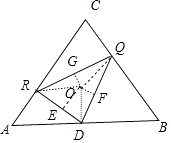

练习册系列答案
相关题目