题目内容
讨论函数f(x)=x+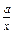 (a>0)的单调性.
(a>0)的单调性.
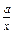 (a>0)的单调性.
(a>0)的单调性.f(x)分别在(-∞,- ]、[
]、[ ,+∞)上为增函数;f(x)分别在[-
,+∞)上为增函数;f(x)分别在[- ,0)、(0,
,0)、(0, ]上为减函数
]上为减函数
 ]、[
]、[ ,+∞)上为增函数;f(x)分别在[-
,+∞)上为增函数;f(x)分别在[- ,0)、(0,
,0)、(0, ]上为减函数
]上为减函数 方法一 显然f(x)为奇函数,所以先讨论函数f(x)在(0,+∞)上的单调性,设x1>x2>0,则
f(x1)-f(x2) =(x1+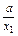 )-(x2+
)-(x2+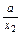 )=(x1-x2)·(1-
)=(x1-x2)·(1-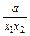 ).
).
∴当0<x2<x1≤ 时,
时,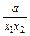 >1,
>1,
则f(x1)-f(x2)<0,即f(x1)<f(x2),故f(x)在(0, ]上是减函数.
]上是减函数.
当x1>x2≥ 时,0<
时,0<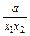 <1,则f(x1)-f(x2)>0,即f(x1)>f(x2),
<1,则f(x1)-f(x2)>0,即f(x1)>f(x2),
故f(x)在[ ,+∞)上是增函数.∵f(x)是奇函数,
,+∞)上是增函数.∵f(x)是奇函数,
∴f(x)分别在(-∞,- ]、[
]、[ ,+∞)上为增函数;f(x)分别在[-
,+∞)上为增函数;f(x)分别在[- ,0)、(0,
,0)、(0, ]上为减函数.
]上为减函数.
方法二 由f ′(x)=1-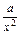 =0可得x=±
=0可得x=±
当x> 时或x<-
时或x<- 时,f ′(x)>0,∴f(x)分别在(
时,f ′(x)>0,∴f(x)分别在( ,+∞)、(-∞,-
,+∞)、(-∞,- ]上是增函数.
]上是增函数.
同理0<x< 或-
或- <x<0时,f′(x)<0
<x<0时,f′(x)<0
即f(x)分别在(0, ]、[-
]、[- ,0)上是减函数.
,0)上是减函数.
f(x1)-f(x2) =(x1+
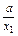 )-(x2+
)-(x2+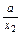 )=(x1-x2)·(1-
)=(x1-x2)·(1-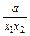 ).
).∴当0<x2<x1≤
 时,
时,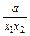 >1,
>1,则f(x1)-f(x2)<0,即f(x1)<f(x2),故f(x)在(0,
 ]上是减函数.
]上是减函数.当x1>x2≥
 时,0<
时,0<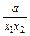 <1,则f(x1)-f(x2)>0,即f(x1)>f(x2),
<1,则f(x1)-f(x2)>0,即f(x1)>f(x2),故f(x)在[
 ,+∞)上是增函数.∵f(x)是奇函数,
,+∞)上是增函数.∵f(x)是奇函数,∴f(x)分别在(-∞,-
 ]、[
]、[ ,+∞)上为增函数;f(x)分别在[-
,+∞)上为增函数;f(x)分别在[- ,0)、(0,
,0)、(0, ]上为减函数.
]上为减函数.方法二 由f ′(x)=1-
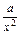 =0可得x=±
=0可得x=±
当x>
 时或x<-
时或x<- 时,f ′(x)>0,∴f(x)分别在(
时,f ′(x)>0,∴f(x)分别在( ,+∞)、(-∞,-
,+∞)、(-∞,- ]上是增函数.
]上是增函数.同理0<x<
 或-
或- <x<0时,f′(x)<0
<x<0时,f′(x)<0即f(x)分别在(0,
 ]、[-
]、[- ,0)上是减函数.
,0)上是减函数.
练习册系列答案
相关题目
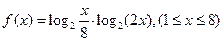 的最大值 和最小值及相应的
的最大值 和最小值及相应的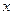 的值.
的值.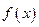 是二次函数,
是二次函数,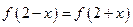 对任意实数
对任意实数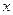 都成立,又知
都成立,又知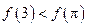 ,求
,求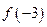 与
与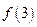 的大小?
的大小?
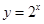
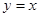
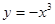
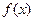 满足:对任意的
满足:对任意的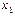 、
、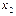
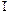
 ,都有
,都有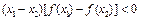 ,则
,则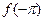 与
与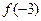 的大小关系是______________________________.
的大小关系是______________________________.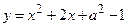 在区间
在区间 上的最大值为
上的最大值为 ,求实数
,求实数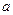 的值.
的值. 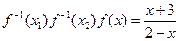
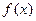 的反函数
的反函数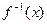 及
及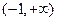 上是增函数
上是增函数 ,则
,则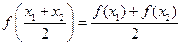 ;
;