题目内容
11.将一根长度为a(a为正常数)的合金做成“田”字形窗户.当窗户的面积最大时,窗户的长宽之比为 ( )| A. | $\sqrt{2}$:1 | B. | $\sqrt{3}$:$\sqrt{2}$ | C. | 1:1 | D. | 2:1 |
分析 设出窗户的长与宽,表示出面积,利用基本不等式求最值,即可求得结论
解答 解:设窗户的长为x,则宽为$\frac{a}{3}$-x,面积设为y.
则y=x×($\frac{a}{3}$-x)≤$(\frac{x+\frac{a}{3}-x}{2})^{2}$=$\frac{{a}^{2}}{36}$
当且仅当x=$\frac{a}{3}$-x,即x=$\frac{a}{6}$时,窗户面积最大,透过的光线最多
此时$\frac{a}{3}$-x=$\frac{a}{6}$
∴窗户的长宽之比为1:1
故选:C.
点评 本题主要考查了基本不等式在最值问题中的应用,确定函数解析式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.已知抛物线x2=2py(p>0)的焦点与双曲线x2-y2=-$\frac{1}{2}$的一个焦点重合,且在抛物线上有一动点P到x轴的距离为m,P到直线l:2x-y-4=0的距离为n,则m+n的最小值为( )
| A. | $\sqrt{5}$+1 | B. | $\sqrt{5}$-1 | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$-2 |
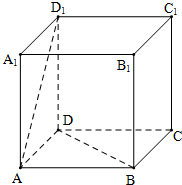 如图,正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12.
如图,正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12. 如图,斜四边形ABCD-A1B1C1D1的底面是边长为8cm的正方形,侧棱AA1成为12cm,且上底面的顶点A1与下底面各点间的距离相等,则四棱柱的侧面积是$32\sqrt{15}$.
如图,斜四边形ABCD-A1B1C1D1的底面是边长为8cm的正方形,侧棱AA1成为12cm,且上底面的顶点A1与下底面各点间的距离相等,则四棱柱的侧面积是$32\sqrt{15}$.