题目内容
3.设A,B是抛物线x2=2py(p>0)两点,且满足$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,(1)求证:直线AB经过一定点
(2)当线段AB的中点到直线y-2x=0的距离的最小值为$\frac{2\sqrt{5}}{5}$,求p的值.
分析 (1)欲证直线经过定点,只需找到直线方程,在验证不管参数为何值都过某一定点即可,可根据直线OA,OB垂直,设AB方程,根据OA,OB垂直消去一些参数,再进行判断;
(2)设AB中点的坐标,根据OA,OB垂直,可得AB中点坐标满足的关系式,再用点到直线的距离公式求AB的中点到直线y-2x=0的距离的,求出最小值,让其为$\frac{2\sqrt{5}}{5}$,解参数p即可.
解答 (1)证明:设A,B两点的坐标为(x1,y1),(x2,y2)
则 x12=2py1,x22=2py2.
经过A,B两点的直线方程为(x2-x1)(y-y1)=(y2-y1)(x-x1).
由y1=$\frac{{{x}_{1}}^{2}}{2p}$,y2=$\frac{{{x}_{2}}^{2}}{2p}$
得(x2-x1)(y-y1)=($\frac{{{x}_{2}}^{2}}{2p}$-$\frac{{{x}_{1}}^{2}}{2p}$)(x-x1).
∵x1≠x2.
令x=0,得y-y1=$\frac{{x}_{1}+{x}_{2}}{2p}$(x-x1),
∴y=-$\frac{{x}_{1}{x}_{2}}{2p}$(*)
∵$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,
∴x1x2+y1y2=0,从而x1x2+$\frac{{{x}_{1}}^{2}{{x}_{2}}^{2}}{4{p}^{2}}$=0.
∵x1x2≠0,∴x1x2=-4p2.
代入(*),得 y=2p,
∴AB始终经过定点(0,2p).
(2)解:设AB中点的坐标为(x,y),
则x1+x2=2x,y1+y2=2y,
∴x12+x22=2py1+2py2=2p(y1+y2).
又∵x12+x22=(x1+x2)2-2x1x2=(x1+x2)2+8p2,
∴4x2+8p2=4py,
即y=$\frac{1}{p}$x2+2p.…①
AB的中点到直线y-2x=0的距离d=$\frac{|y-2x|}{\sqrt{5}}$.
将①代入,得d=$\frac{|\frac{1}{p}{x}^{2}-2x+2p|}{\sqrt{5}}$=$\frac{\frac{1}{p}(x-p)^{2}+p}{\sqrt{5}}$,
因为d的最小值为$\frac{2\sqrt{5}}{5}$,
∴当x=p时,取得最小值$\frac{p}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∴p=2.
点评 本题考查抛物线的方程和应用,主要考查了直线与抛物线的位置关系的判断,注意韦达定理的应用,同时考查直线恒过定点的求法,属于中档题.

| A. | $\sqrt{2}$:1 | B. | $\sqrt{3}$:$\sqrt{2}$ | C. | 1:1 | D. | 2:1 |
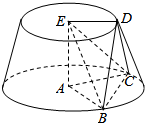 如图圆台的上下底面的圆心分别是E、A,点D在上底面圆周上,B、C在下底面圆周上,已知EA=1,ED=$\sqrt{3}$,AC=BC=2,BD=CD.
如图圆台的上下底面的圆心分别是E、A,点D在上底面圆周上,B、C在下底面圆周上,已知EA=1,ED=$\sqrt{3}$,AC=BC=2,BD=CD.