题目内容
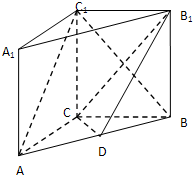
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求证:AC1∥平面CDB1;
(Ⅲ)若BB1=4,求CB1与平面AA1B1B所成角的正切值.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求证:AC1∥平面CDB1;
(Ⅲ)若BB1=4,求CB1与平面AA1B1B所成角的正切值.

(Ⅰ) 证明:∵三棱柱ABC-A1B1C1为直三棱柱,
∴C1C⊥平面ABC,∴C1C⊥AC,
∵AC=3,BC=4,AB=5,
∴AC⊥BC,
又C1C∩BC=C,
∴AC⊥平面CC1B1B,
∵BC1?平面CC1B1B,
∴AC⊥BC1;
(Ⅱ)证明:令BC1与CB1的交点为E,连结DE.
∵D是AB的中点,E为BC1的中点,
∴DE∥AC1,
又∵AC1?平面CDB1,DE?平面CDB1,
∴AC1∥平面CDB1;
(Ⅲ)作CD⊥AB于D,连B1D,则
∴CD⊥BB1,AB∩BB1=B,
∴CD⊥平面A1B,
∴∠CB1D即为 CB1与平面AA1B1B所成角,
在直角△ABC中,由等面积可得CD=
,
∵BB1=4,BC=4,
∴CB1=4
,
∴B1D=
∴tan∠CB1D=
=
.

∴C1C⊥平面ABC,∴C1C⊥AC,
∵AC=3,BC=4,AB=5,
∴AC⊥BC,
又C1C∩BC=C,
∴AC⊥平面CC1B1B,
∵BC1?平面CC1B1B,
∴AC⊥BC1;
(Ⅱ)证明:令BC1与CB1的交点为E,连结DE.
∵D是AB的中点,E为BC1的中点,
∴DE∥AC1,
又∵AC1?平面CDB1,DE?平面CDB1,
∴AC1∥平面CDB1;
(Ⅲ)作CD⊥AB于D,连B1D,则
∴CD⊥BB1,AB∩BB1=B,
∴CD⊥平面A1B,
∴∠CB1D即为 CB1与平面AA1B1B所成角,
在直角△ABC中,由等面积可得CD=
| 12 |
| 5 |
∵BB1=4,BC=4,
∴CB1=4
| 2 |
∴B1D=
4
| ||
| 5 |
∴tan∠CB1D=
| CD |
| B1D |
3
| ||
| 41 |


练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目