题目内容

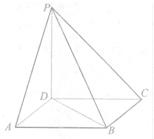
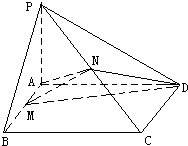
如图，在四棱锥P-ABCD中，PA⊥面ABCD，AB=BC=2，AD=CD=
7
，PA=
3
，∠ABC=120°，G为线段PC的中点．
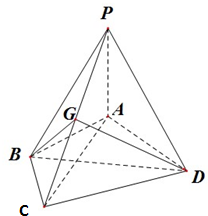
（1）证明：PA∥平面BGD；
（2）求直线DG与平面PAC所成的角的正切值．
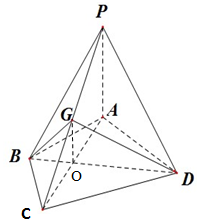
（1）证明：设点O为AC、BD的交点，由AB=BC，AD=CD，得BD是线段AC的中垂线，所以O为AC的中点，
连结OG，
因为G为PC的中点，所以OG∥PA，
又因为PA?平面BGD，OG?平面BGD，
所以PA∥面BGD；
（2）因为PA⊥平面ABCD，BD?平面ABCD，
∴BD⊥PA，
又由（1）知BD⊥AC，PA∩AC=A，
所以BD⊥平面PAC，
所以DG与面PAC所成的角是∠DGO．
由（1）知：OG=
1
2
PA=
3
2
，在△ABC中，AC=
AB2+BC2-2AB•BC•cos∠ABC
=2
3
，
所以OC=
1
2
AC=
3
，
在直角△OCD中，OD=
CD2-OC2
=2，
在直角△OGD中，tan∠DGO=
OD
OG
=
4
3
3
，
所以直线DG与面PAC所成的角的正切值是
4
3
3
．
练习册系列答案
相关题目
如图在长方体ABCD-A1B1C1D1中，AB=a，AD=b，AC1=c，点M为AB的中点，点N为BC的中点．
（1）求长方体ABCD-A1B1C1D1的体积；
（2）若a=4，b=2，c=
21
，求异面直线A1M与B1N所成的角．
如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，点D是AB的中点．
（Ⅰ）求证：AC⊥BC1；
（Ⅱ）求证：AC1∥平面CDB1；
（Ⅲ）若BB1=4，求CB1与平面AA1B1B所成角的正切值．
如图，四棱锥S-ABCD中，底面ABCD是边长为4的正方形，O是AC与BD的交点，SO⊥平面ABCD，E是侧棱SC的中点，异面直线SA和BC所成角的大小是60°．
（Ⅰ）求证：直线SA∥平面BDE；
（Ⅱ）求直线BD与平面SBC所成角的正弦值．
如图，四棱锥P-ABCD的底面ABCD为一直角梯形，侧面PAD是等边三角形，其中BA⊥AD，CD⊥AD，CD=2AD=2AB，平面PAD⊥底面ABCD，E是PC的中点．
（1）求证：BE∥平面PAD；
（2）求证：BE⊥CD；
（3）求BD与平面PDC所成角的正弦值．
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD=AD=2．
（1）求PC与平面PBD所成的角；
（2）在线段PB上是否存在一点E，使得PC⊥平面ADE？并说明理由．

四棱锥S-ABCD的底面ABCD是正方形，侧棱SC的中点E在底面内的射影恰好是正方形ABCD的中心O，顶点A在截面SBD内的射影恰好是△SBD的重心G．
（1）求直线SO与底面ABCD所成角的正切值；
（2）设AB=a，求此四棱锥过点C，D，G的截面面积．
正方体ABCD-A1B1C1D1中二面角A1-BD-C1的余弦值为______．
如图，已知ABCD是矩形，PA⊥平面ABCD，M，N分别是AB，PC的中点，PA=2，PD=AB，且平面MND⊥平面PCD．
（1）求证：MN⊥AB；
（2）求二面角P-CD-A的大小；
（3）求三棱锥D-AMN的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网