题目内容

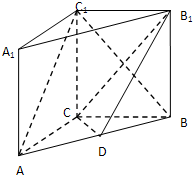
正方体ABCD-A1B1C1D1中直线A1D与平面AB1C1D所成角为（　　）
A．30°B．45°C．60°D．90°
∵正方体ABCD-A1B1C1D中
有：A1B⊥AB1，AD⊥A1B⇒A1B⊥平面AB1C1D；
所以：直线A1D与平面AB1C1D所成的角为∠ODA1；
∵A1B=BD=A1D
∴∠BDA1=60°；
故∠ODA1=
1
2

∴∠BDA1=30°．
故选A
练习册系列答案
相关题目
过正方体ABCD-A1B1C1D1的顶点A作直线L，使L与棱AB，AD，AA1所成的角都相等，这样的直线L可以作（　　）
A．1条B．2条C．3条D．4条
如图：四面体A-BCD被一平面所截，截面EFHG是一个矩形，
（1）求证：AB∥FH；
（2）求异面直线AB、CD所成的角．
如图在长方体ABCD-A1B1C1D1中，AB=a，AD=b，AC1=c，点M为AB的中点，点N为BC的中点．
（1）求长方体ABCD-A1B1C1D1的体积；
（2）若a=4，b=2，c=
21
，求异面直线A1M与B1N所成的角．
已知正△ABC的顶点A在平面α内，顶点B，C在平面α的同一侧，D为BC的中点，若△ABC在平面α内的射影是以A为直角顶点的三角形，则直线AD与平面α所成角的正弦值的最小值为______．
已知平面α∥β，A，C∈α，B，D∈β，AB⊥CD，且AB=2，直线AB与平面α所成的角为60°，则线段CD长的取值范围为（　　）
A．[2，+∞）B．[2C．[2
3
，+∞)		D．[2
3
，4]
如图，正三棱柱的九条棱都相等，三个侧面都是正方体，M、N分别是BC和A1C1的中点，求MN与CC1所成角的余弦值．
如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，点D是AB的中点．
（Ⅰ）求证：AC⊥BC1；
（Ⅱ）求证：AC1∥平面CDB1；
（Ⅲ）若BB1=4，求CB1与平面AA1B1B所成角的正切值．

四棱锥S-ABCD的底面ABCD是正方形，侧棱SC的中点E在底面内的射影恰好是正方形ABCD的中心O，顶点A在截面SBD内的射影恰好是△SBD的重心G．
（1）求直线SO与底面ABCD所成角的正切值；
（2）设AB=a，求此四棱锥过点C，D，G的截面面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网